题目内容
已知双曲线的两条渐近线方程为3x±4y=0,则双曲线方程为
-
=±λ(λ>0)
-
=±λ(λ>0).
| x2 |
| 16 |
| y2 |
| 9 |
| x2 |
| 16 |
| y2 |
| 9 |
分析:只知渐近线不知焦点,欲求双曲线方程,故分两种情况(焦点分别在x轴和y轴上)即可得
-
=±λ(λ>0).
| x2 |
| 16 |
| y2 |
| 9 |
解答:解:①当双曲线焦点在x轴上时,
∵已知双曲线的两条渐近线方程为3x±4y=0,
得双曲线方程为
-
=λ(λ>0).
②当双曲线焦点在y轴上时,
∵已知双曲线的两条渐近线方程为3x±4y=0,
得双曲线方程为
-
=-λ(λ>0).
故答案为:
-
=±λ(λ>0).
∵已知双曲线的两条渐近线方程为3x±4y=0,
得双曲线方程为
| x2 |
| 16 |
| y2 |
| 9 |
②当双曲线焦点在y轴上时,
∵已知双曲线的两条渐近线方程为3x±4y=0,
得双曲线方程为
| x2 |
| 16 |
| y2 |
| 9 |
故答案为:
| x2 |
| 16 |
| y2 |
| 9 |
点评:本小题主要考查双曲线的标准方程、双曲线的简单性质等基础知识,考查运算求解能力.若双曲线的渐近线方程为ax±by=0,可设双曲线方程为
-
=λ,λ≠0.
| x2 |
| b2 |
| y2 |
| a2 |

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,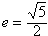 。
。