题目内容
已知函数 ,数列{an}满足a1=a(a≠-2,a∈R),
,数列{an}满足a1=a(a≠-2,a∈R),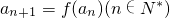 .
.
(Ⅰ)若数列{an}是常数列,求a的值;
(Ⅱ)当a1= 时,记
时,记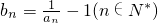 ,证明数列{bn}是等比数列,并求出{bn}的通项公式.
,证明数列{bn}是等比数列,并求出{bn}的通项公式.
解:(Ⅰ)依题意得,an+1=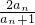 ,
,
∵a1=a(a≠-2,a∈R),数列{an}是常数列,
∴an+1=an=a,
∴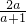 =a,
=a,
∴a=1或a=0(舍),
∴a=1;
(Ⅱ)证明∵an+1=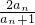 ,
,
∴ =
= =
= +
+ ,
,
∴ -1=
-1= (
( -1),又bn=
-1),又bn= -1(n∈N*),
-1(n∈N*),
∴bn+1= bn,
bn,
∴ =
= ,又a1=
,又a1= ,b1=
,b1= -1=
-1= ,
,
∴数列{bn}是以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,
∴bn= •
• =
= .
.
分析:(Ⅰ)若数列{an}是常数列,则a2=a1=a,即可求得a的值;
(Ⅱ)当a1= 时,可求得
时,可求得 =
= ,利用等比数列的概念可证明数列{bn}是等比数列,从而可求得{bn}的通项公式.
,利用等比数列的概念可证明数列{bn}是等比数列,从而可求得{bn}的通项公式.
点评:本题考查等比关系的确定,考查等比数列的通项公式,证明数列{bn}是等比数列是难点所在,考查转化与运算能力,属于中档题.
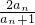 ,
,∵a1=a(a≠-2,a∈R),数列{an}是常数列,
∴an+1=an=a,
∴
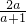 =a,
=a,∴a=1或a=0(舍),
∴a=1;
(Ⅱ)证明∵an+1=
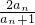 ,
,∴
 =
= =
= +
+ ,
,∴
 -1=
-1= (
( -1),又bn=
-1),又bn= -1(n∈N*),
-1(n∈N*),∴bn+1=
 bn,
bn,∴
 =
= ,又a1=
,又a1= ,b1=
,b1= -1=
-1= ,
,∴数列{bn}是以
 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,∴bn=
 •
• =
= .
.分析:(Ⅰ)若数列{an}是常数列,则a2=a1=a,即可求得a的值;
(Ⅱ)当a1=
 时,可求得
时,可求得 =
= ,利用等比数列的概念可证明数列{bn}是等比数列,从而可求得{bn}的通项公式.
,利用等比数列的概念可证明数列{bn}是等比数列,从而可求得{bn}的通项公式.点评:本题考查等比关系的确定,考查等比数列的通项公式,证明数列{bn}是等比数列是难点所在,考查转化与运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,数列an满足
,数列an满足 .
.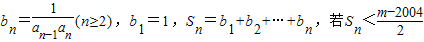 对一切n∈N*成立,求最小正整数m.
对一切n∈N*成立,求最小正整数m.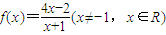 ,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an. 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( ) ,1) B.(
,1) B.(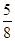 ) C.(
) C.( ) D.(
) D.( ,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是
,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是