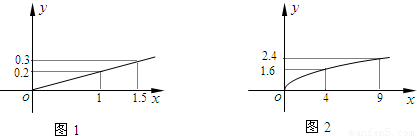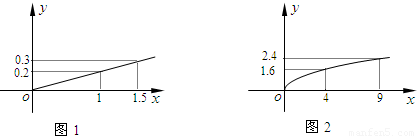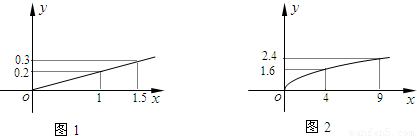��Ŀ����
ijͶ�ʹ�˾�ƻ�Ͷ��A��B���ֽ��ڲ�Ʒ�������г�������Ԥ�⣬A��Ʒ������y��Ͷ����x�������������ϵ��ͼ1��B��Ʒ������y��Ͷ����x������ƽ�����������������ϵ��ͼ2����ע��������Ͷ������λ����Ԫ��
��1���ֱ�A��B����Ʒ�������ʾΪͶ�����ĺ�����ϵʽ��
��2���ù�˾����10��Ԫ�ʽ𣬲�ȫ��Ͷ��A��B���ֲ�Ʒ�У��ʣ�����������10��ԪͶ�ʣ�����ʹ��˾�������������������Ϊ������Ԫ��
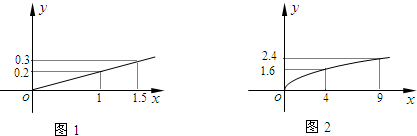
��1���ֱ�A��B����Ʒ�������ʾΪͶ�����ĺ�����ϵʽ��
��2���ù�˾����10��Ԫ�ʽ𣬲�ȫ��Ͷ��A��B���ֲ�Ʒ�У��ʣ�����������10��ԪͶ�ʣ�����ʹ��˾�������������������Ϊ������Ԫ��
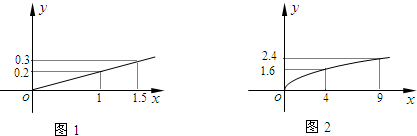
��������1������A��Ʒ������y��Ͷ����x����������B��Ʒ������y��Ͷ����x������ƽ���������������ʿ��躯����ϵʽ������ͼ���е�����㣬����������ʽ��
��2����A��ƷͶ��x��Ԫ����B��ƷͶ��10-x��Ԫ������ҵ����Ϊy��Ԫ�����ã�1���ɴ˿ɽ������������û�Ԫ����ת��Ϊ���κ����������䷽����������ֵ��
��2����A��ƷͶ��x��Ԫ����B��ƷͶ��10-x��Ԫ������ҵ����Ϊy��Ԫ�����ã�1���ɴ˿ɽ������������û�Ԫ����ת��Ϊ���κ����������䷽����������ֵ��
����⣺��1����Ͷ��Ϊx��Ԫ��A��Ʒ������Ϊf��x����Ԫ��B��Ʒ������Ϊg��x����Ԫ��
��������f��x��=k1x��g(x)=k2
����ͼ֪f(1)=
����k1=
��g��4��=1.6����k2=
���Ӷ�f(x)=
x(x��0)��g(x)=
(x��0)��8�֣�
��2����A��ƷͶ��x��Ԫ����B��ƷͶ��10-x��Ԫ������ҵ����Ϊy��Ԫ��
y=f(x)+g(10-x)=
+
��0��x��10��
��
=t����y=
+
t=-
(t-2)2+
(0��t��
)
��t=2ʱ��ymax=
=2.8����ʱx=10-4=6��15�֣�
�𣺵�A��ƷͶ��6��Ԫ����B��ƷͶ��4��Ԫʱ��
����ҵ��������������Ϊ2.8��Ԫ�� ��16�֣�
��������f��x��=k1x��g(x)=k2
| x |
| 1 |
| 5 |
| 1 |
| 5 |
��g��4��=1.6����k2=
| 4 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| x |
��2����A��ƷͶ��x��Ԫ����B��ƷͶ��10-x��Ԫ������ҵ����Ϊy��Ԫ��
y=f(x)+g(10-x)=
| x |
| 5 |
| 4 |
| 5 |
| 10-x |
��
| 10-x |
| 10-t2 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 14 |
| 5 |
| 10 |
��t=2ʱ��ymax=
| 14 |
| 5 |
�𣺵�A��ƷͶ��6��Ԫ����B��ƷͶ��4��Ԫʱ��
����ҵ��������������Ϊ2.8��Ԫ�� ��16�֣�
����������Ŀ����Ǻ���ģ�͵�ѡ����Ӧ�ã���Ҫ��������������ģ�ͣ��ؼ��ǽ�ʵ������ת��Ϊ��ѧ���⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ