题目内容
已知a，b∈R+，函数f(x)=
(x∈R)．
（1）判断函数f（x）的单调性，并证明你的结论；
（2）比较
与
的大小．
| ax+1+bx+1 |
| ax+bx |
（1）判断函数f（x）的单调性，并证明你的结论；
（2）比较
| a2+b2 |
| a+b |
| ab |
分析：（1）利用函数单调性的定义证明．（2）通过作差法判断大小．
解答：解：（1）函数f(x)=
(x∈R)递增函数，证明如下：
设x＜y，则x-y＜0，f(x)-f(y)=
，
①当a=b时，f（x）为常数函数，此时不单调．
②若a＞b，则a-b＞0，ax-y＜bx-y，ax-y-bx-y＜0，所以f（x）＜f（y），
此时函数f(x)=
(x∈R)递增函数．
③当a＜b，则a-b＜0，ax-y＞bx-y，ax-y-bx-y＞0，所以f（x）＜f（y），
此时函数f(x)=
(x∈R)递增函数．
（2）
-
=
=
=
，
因为幂函数x
，x
在（0，+∞）上单调递增，具有相同的单调性．
所以当a=b时，
=
．
当a≠b时，
＞
．
| ax+1+bx+1 |
| ax+bx |
设x＜y，则x-y＜0，f(x)-f(y)=
| (a-b)(ax-y-bx-y)ayby |
| (ax+bx)(ay+by) |
①当a=b时，f（x）为常数函数，此时不单调．
②若a＞b，则a-b＞0，ax-y＜bx-y，ax-y-bx-y＜0，所以f（x）＜f（y），
此时函数f(x)=
| ax+1+bx+1 |
| ax+bx |
③当a＜b，则a-b＜0，ax-y＞bx-y，ax-y-bx-y＞0，所以f（x）＜f（y），
此时函数f(x)=
| ax+1+bx+1 |
| ax+bx |
（2）
| a2+b2 |
| a+b |
| ab |
a2+b2-a
| ||||
| a+b |
a2+b2-a
| ||||||||
| a+b |
(a
| ||||||||
| a+b |
因为幂函数x
| 3 |
| 2 |
| 1 |
| 2 |
所以当a=b时，
| a2+b2 |
| a+b |
| ab |
当a≠b时，
| a2+b2 |
| a+b |
| ab |
点评：本题的考点是利用作差法比较两个数的大小以及利用单调性的定义去判断函数的单调性，作差法是比较大小中最常用的一种方法．
练习册系列答案
相关题目
=（x，1），
=（-1，b-x），函数f（x）=a-
是偶函数．
=（x，1），
=（-1，b-x），函数f（x）=a-
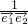是偶函数．