题目内容
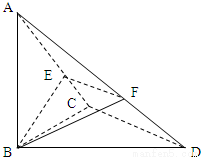
(理)已知ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且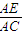 =
=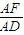 =λ(0<λ<1).
=λ(0<λ<1).(1)求证不论λ为何值,总有平面BEF⊥平面ABC;
(2)若平面BEF与平面BCD所成的二面角的大小为60°,求λ的值.
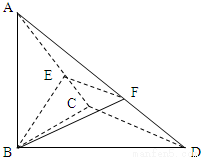
【答案】分析:(1)由已知中,∠BCD=90°,AB⊥平面BCD,我们易得到CD⊥平面ABC,又由E、F分别是AC、AD上的动点,且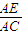 =
=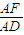 =λ,故EF∥CD即EF⊥平面ABC,再由面面垂直的判定定理,即可得到答案.
=λ,故EF∥CD即EF⊥平面ABC,再由面面垂直的判定定理,即可得到答案.
(2)过点C作CZ∥AB,以C为原点,建立空间直角坐标系C-xyz.分别求出各顶点的坐标,并根据ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,分别求出平面BEF的法向量和平面BCD的法向量,然后根据平面BEF与平面BCD所成的二面角的大小为60°,代入向量夹角公式,构造一个关于λ的方程,解方程即可得到平面BEF与平面BCD所成的二面角的大小为60°时λ的值.
解答: 解:(1)∵AB⊥平面BCD,
解:(1)∵AB⊥平面BCD,
∴AB⊥CD,
又在△BCD中,∠BCD=90°,
∴BC⊥CD,又AB∩BC=B,
∴CD⊥平面ABC,
又在△ACD中E、F分别是AC、AD上的动点,且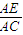 =
=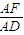 =λ,
=λ,
∴EF∥CD,
∴EF⊥平面ABC,又EF?平面BEF,
∴不论λ为何值,总有平面BEF⊥平面ABC;
(2)过点C作CZ∥AB,∵AB⊥平面BCD,
∴CZ⊥平面BCD,
又在△BCD中,∠BCD=90°,
∴BC⊥CD,
如图,以C为原点,建立空间直角坐标系C-xyz.
又在△BCD中,∠BCD=90°,BC=CD=1,
∴BD=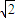 .
.
又在Rt△ABD中,∠ADB=60°,
∴AB=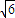 ,
,
则C(0,0,0),B(1,0,0),A(1,0, ),D(0,1,0).
),D(0,1,0).
∵ =
= =λ,∴
=λ,∴ ,
,
∵ =(-1,0,-
=(-1,0,- ),∴
),∴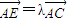 =(λ,0,-
=(λ,0,-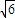 λ),
λ),
又∵ =(0,0,-
=(0,0,-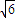 ),∴
),∴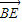 =
=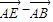 =(-λ,0,
=(-λ,0, (1-λ)),
(1-λ)),
设 =(x,y,z)是平面BEF的法向量,则
=(x,y,z)是平面BEF的法向量,则 ,
, ,
,
因为EF∥CD,所以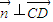 ,因为
,因为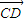 =(0,1,0),
=(0,1,0),
所以 ,
,
令z=λ得x=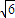 (1-1λ),y=0,
(1-1λ),y=0, =(
=(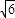 (1-1λ),0,λ),
(1-1λ),0,λ),
因为 =(0,0,1)是平面BCD的法向量,且平面BEF与平面BCD所成的二面角为60°,
=(0,0,1)是平面BCD的法向量,且平面BEF与平面BCD所成的二面角为60°,
∴cos60°= =
= =
=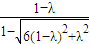 ,
,
∴λ2-4λ+2=0,
∴ 或
或 (不合题意,舍去),
(不合题意,舍去),
故当平面BEF与平面BCD所成的二面角为60°,时 .
.
点评:本题考查的知识点是平面与平面垂直的判定,用空间向量求平面间的夹角,其中在(2)中,构造适当的空间坐标系,然后结合向量法求二面角的方法,构造一个关于λ的方程,是解答本题的关键.
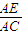 =
=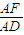 =λ,故EF∥CD即EF⊥平面ABC,再由面面垂直的判定定理,即可得到答案.
=λ,故EF∥CD即EF⊥平面ABC,再由面面垂直的判定定理,即可得到答案.(2)过点C作CZ∥AB,以C为原点,建立空间直角坐标系C-xyz.分别求出各顶点的坐标,并根据ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,分别求出平面BEF的法向量和平面BCD的法向量,然后根据平面BEF与平面BCD所成的二面角的大小为60°,代入向量夹角公式,构造一个关于λ的方程,解方程即可得到平面BEF与平面BCD所成的二面角的大小为60°时λ的值.
解答:
 解:(1)∵AB⊥平面BCD,
解:(1)∵AB⊥平面BCD,∴AB⊥CD,
又在△BCD中,∠BCD=90°,
∴BC⊥CD,又AB∩BC=B,
∴CD⊥平面ABC,
又在△ACD中E、F分别是AC、AD上的动点,且
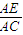 =
=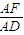 =λ,
=λ,∴EF∥CD,
∴EF⊥平面ABC,又EF?平面BEF,
∴不论λ为何值,总有平面BEF⊥平面ABC;
(2)过点C作CZ∥AB,∵AB⊥平面BCD,
∴CZ⊥平面BCD,
又在△BCD中,∠BCD=90°,
∴BC⊥CD,
如图,以C为原点,建立空间直角坐标系C-xyz.
又在△BCD中,∠BCD=90°,BC=CD=1,
∴BD=
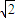 .
.又在Rt△ABD中,∠ADB=60°,
∴AB=
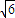 ,
,则C(0,0,0),B(1,0,0),A(1,0,
 ),D(0,1,0).
),D(0,1,0).∵
 =
= =λ,∴
=λ,∴ ,
,∵
 =(-1,0,-
=(-1,0,- ),∴
),∴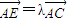 =(λ,0,-
=(λ,0,-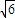 λ),
λ),又∵
 =(0,0,-
=(0,0,-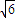 ),∴
),∴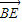 =
=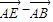 =(-λ,0,
=(-λ,0, (1-λ)),
(1-λ)),设
 =(x,y,z)是平面BEF的法向量,则
=(x,y,z)是平面BEF的法向量,则 ,
, ,
,因为EF∥CD,所以
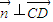 ,因为
,因为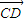 =(0,1,0),
=(0,1,0),所以
 ,
,令z=λ得x=
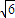 (1-1λ),y=0,
(1-1λ),y=0, =(
=(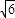 (1-1λ),0,λ),
(1-1λ),0,λ),因为
 =(0,0,1)是平面BCD的法向量,且平面BEF与平面BCD所成的二面角为60°,
=(0,0,1)是平面BCD的法向量,且平面BEF与平面BCD所成的二面角为60°,∴cos60°=
 =
= =
=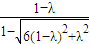 ,
,∴λ2-4λ+2=0,
∴
 或
或 (不合题意,舍去),
(不合题意,舍去),故当平面BEF与平面BCD所成的二面角为60°,时
 .
.点评:本题考查的知识点是平面与平面垂直的判定,用空间向量求平面间的夹角,其中在(2)中,构造适当的空间坐标系,然后结合向量法求二面角的方法,构造一个关于λ的方程,是解答本题的关键.

练习册系列答案
相关题目
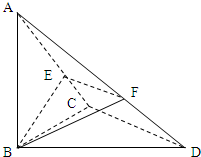 (理)已知ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
(理)已知ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
 (理)已知函数
(理)已知函数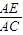 =
=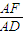 =λ(0<λ<1).
=λ(0<λ<1).