题目内容
某中学对高二甲、乙两个同类班级进行加强语文阅读理解训练对提高数学应用题得分率作用的试验，其中甲班为实验班（常规教学，无额外训练），在试验前的测试中，甲、乙两班学生在数学应用题上的得分率基本一致，试验结束后，统计几次数学应用试题测试的平均成绩（均取整数）如表所示：
| | 60分以下 | 61﹣70分 | 71﹣80分 | 81﹣90分 | 91﹣100分 |
| 甲班（人数） | 3 | 6 | 11 | 18 | 12 |
| 乙班（人数） | 3 | 9 | 13 | 15 | 10 |
现规定平均成绩在80分以上（不含80分）的为优秀．
（1）试分析估计两个班级的优秀率；
（2）由以上统计列出2×2列联表．
（1）甲、乙两班的优秀率分别为60%和50%．；（2） 优秀人数 非优秀人数 合计 甲班 30 20 50 乙班 25 25 50 合计 55 45 100
解析试题分析：（1）根据所给的表格，看出两个班的所有的人数和两个班优秀的人数，分别用两个班优秀的人数除以总人数，得到两个班的优秀率．
（2）根据所给的数据列出列联表．
试题解析：（1）由题意，甲、乙两班均有学生50人，
甲班优秀人数为30人，优秀率为
，乙班优秀人数为25人，优秀率为
∴甲、乙两班的优秀率分别为60%和50%．
（2）根据题意做出列联表 优秀人数 非优秀人数 合计 甲班 30 20 50 乙班 25 25 50 合计 55 45 100
考点：１．独立性检验．
练习册系列答案
阅读快车系列答案
相关题目
某企业职工的月工资数统计如下：
| 月工资数（元） | 10000 | 8000 | 5500 | 2500 | 1600 | 1200 | 900 | 600 | 500 |
| 得此工资人数 | 1 | 3 | 3 | 8 | 20 | 35 | 45 | 3 | 2 |
请你站在其中一立场说明理由： 。
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本，得频率分布表如下：
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | 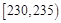 | 8 | 0．16 |
| 第二组 | 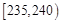 | ① | 0．24 |
| 第三组 | 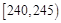 | 15 | ② |
| 第四组 | 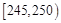 | 10 | 0．20 |
| 第五组 | 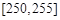 | 5 | 0．10 |
| 合 计 | 50 | 1．00 | |
（１）写出表中①②位置的数据；
（２）为了选拔出更优秀的学生，高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核，分别求第三、四、五各组参加考核人数；
（３）在（２）的前提下，高校决定在这6名学生中录取2名学生，求2人中至少有1名是第四组的概率．
（本小题满分12分）
海关对同时从
三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如右表所示，工作人员用分层抽样的方法从这些商品中共抽取6件进行检测
| 地区 |  |  |  |
| 数量 | 50 | 150 | 100 |
（1）求这6件样品中来自
各地区商品的数量；（2）若在这6件样品中随机抽取2件送往甲机构进一步检测，求这2件商品来自相同地区的概率.
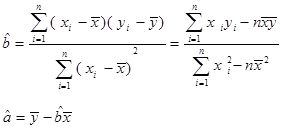
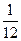，则总体中的个体数为 。