题目内容
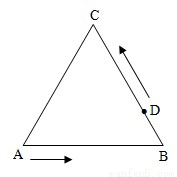
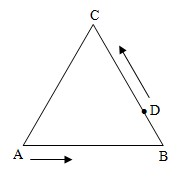例2：如图：△ABC是边长为3厘米的正三角形，D是BC边上靠近点B的三等分点，甲、乙两个质点分别从点A、D同时出发，都以1厘米/秒的速度按图示方向沿三角形的边作匀速运动，经过时间t（0≤t≤3）秒后，两质点的距离为S（t）．（1）写出函数S（t）
（2）求S（t）的最大值和最小值，并求取得最大值、最小值时相应的t的值．
分析：（1）设A，D分别运动到E，F，由于0≤t≤2时，E在AB上，F在BC上，故在三角形BEF中，利用余弦定理可得s(t)=
；同理2≤t≤3时，E在AB上，F在AC上，则三角形AEF中可求；
（2）先分段求函数的最值，当0≤t≤2时，s(t)=
=
，可知函数的最值，同理当2≤t≤3时，s(t)=
=
，可知函数的最值，再比较可得S（t）的最大值和最小值从而求出相应的t的值．
| BE2+BF2-2×BE×BF×cos60° |
（2）先分段求函数的最值，当0≤t≤2时，s(t)=
| 3t2-9t+9 |
3(t-
|
| 3t2-15t+25 |
3(t-
|
解答：解：（1）设A，D分别运动到E，F，则
当0≤t≤2时，s(t)=
=
当2≤t≤3时，s(t)=
=
∴S(t)=
（2）当0≤t≤2时，s(t)=
=
，
∴S（t）的最大值和最小值分别为3，
；
当2≤t≤3时，s(t)=
=
∴S（t）的最大值和最小值分别为
，
∴S（t）的最大值和最小值分别为3，
；相应的t的值为0，
当0≤t≤2时，s(t)=
| BE2+BF2-2×BE×BF×cos60° |
| 3t2-9t+9 |
当2≤t≤3时，s(t)=
| AE2+AF2-2×AE×AF×cos60° |
| 3t2-15t+25 |
∴S(t)=
|
（2）当0≤t≤2时，s(t)=
| 3t2-9t+9 |
3(t-
|
∴S（t）的最大值和最小值分别为3，
| 3 |
| 2 |
| 3 |
当2≤t≤3时，s(t)=
| 3t2-15t+25 |
3(t-
|
∴S（t）的最大值和最小值分别为
| 7 |
| 5 |
| 2 |
| 3 |
∴S（t）的最大值和最小值分别为3，
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
点评：本题以实际问题为载体，考查函数模型的构建，考查余弦定理的运用，同时考查了分段函数的最值，综合性强．
练习册系列答案
相关题目
