题目内容
在平面直角坐标系xOy中,经过点 且斜率为k的直线l与椭圆
且斜率为k的直线l与椭圆 有两个不同的交点P和Q.
有两个不同的交点P和Q.(Ⅰ)求k的取值范围;
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k,使得向量
 与
与 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.
【答案】分析:(1)直线l与椭圆有两个不同的交点,即方程组有2个不同解,转化为判别式大于0.
(2)利用2个向量共线时,坐标之间的关系,由一元二次方程根与系数的关系求两根之和,解方程求常数k.
解答:解:(Ⅰ)由已知条件,直线l的方程为 ,
,
代入椭圆方程得 .
.
整理得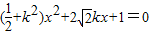 ①
①
直线l与椭圆有两个不同的交点P和Q等价于 ,
,
解得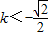 或
或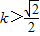 .即k的取值范围为
.即k的取值范围为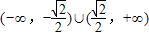 .
.
(Ⅱ)设P(x1,y1),Q(x2,y2),则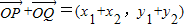 ,
,
由方程①, . ②
. ②
又 . ③
. ③
而 .
.
所以 与
与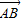 共线等价于
共线等价于 ,
,
将②③代入上式,解得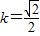 .
.
由(Ⅰ)知 或
或 ,
,
故没有符合题意的常数k.
点评:(1)把直线l与椭圆有两个不同的交点,转化为方程组有2个不同解.
(2)考查2个向量共线的条件.
(2)利用2个向量共线时,坐标之间的关系,由一元二次方程根与系数的关系求两根之和,解方程求常数k.
解答:解:(Ⅰ)由已知条件,直线l的方程为
 ,
,代入椭圆方程得
 .
.整理得
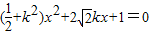 ①
①直线l与椭圆有两个不同的交点P和Q等价于
 ,
,解得
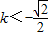 或
或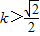 .即k的取值范围为
.即k的取值范围为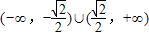 .
.(Ⅱ)设P(x1,y1),Q(x2,y2),则
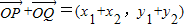 ,
,由方程①,
 . ②
. ②又
 . ③
. ③而
 .
.所以
 与
与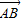 共线等价于
共线等价于 ,
,将②③代入上式,解得
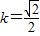 .
.由(Ⅰ)知
 或
或 ,
,故没有符合题意的常数k.
点评:(1)把直线l与椭圆有两个不同的交点,转化为方程组有2个不同解.
(2)考查2个向量共线的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是