题目内容
已知函数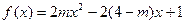 ,
,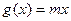 ,设集合
,设集合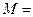 {
{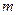
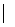
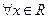 ,
,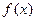
 与
与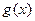 的值中至少有一个为正数}.
的值中至少有一个为正数}.
(Ⅰ)试判断实数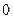 是否在集合
是否在集合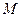 中,并给出理由;
中,并给出理由;
(Ⅱ)求集合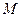 .
.
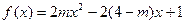 ,
,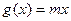 ,设集合
,设集合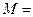 {
{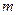
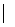
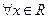 ,
,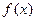
 与
与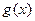 的值中至少有一个为正数}.
的值中至少有一个为正数}.(Ⅰ)试判断实数
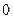 是否在集合
是否在集合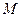 中,并给出理由;
中,并给出理由;(Ⅱ)求集合
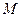 .
.(本小题共15分)
解:(Ⅰ)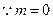 时,
时,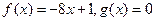 ,
,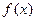 的值不恒为
的值不恒为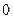 .∴
.∴ 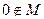 .
.
(Ⅱ)①当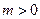 时,
时,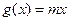 在
在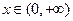 时恒为正,
时恒为正,
∴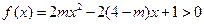 对
对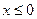 恒成立.
恒成立.
∴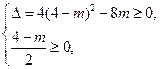 或
或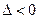 ,
,
解得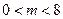 .
.
②当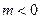 时,
时,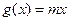 在
在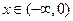 时恒为正,
时恒为正,
∴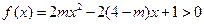 对
对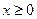 恒成立.
恒成立.
∵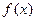 的图象开口向下且过点
的图象开口向下且过点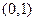 ,
,
∴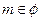 .
.
综上,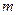 的取值范围是
的取值范围是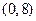 .
.

解:(Ⅰ)
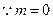 时,
时,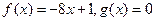 ,
,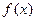 的值不恒为
的值不恒为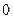 .∴
.∴ 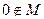 .
.(Ⅱ)①当
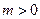 时,
时,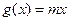 在
在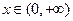 时恒为正,
时恒为正,∴
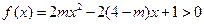 对
对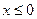 恒成立.
恒成立.∴
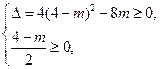 或
或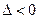 ,
,解得
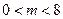 .
.②当
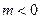 时,
时,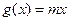 在
在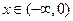 时恒为正,
时恒为正,∴
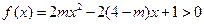 对
对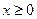 恒成立.
恒成立.∵
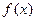 的图象开口向下且过点
的图象开口向下且过点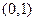 ,
,∴
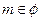 .
.综上,
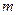 的取值范围是
的取值范围是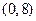 .
.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =( )
=( )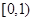

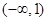
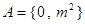 ,
,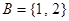 ,则“
,则“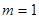 ”是“
”是“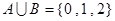 ”的( )
”的( )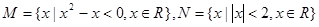 ,则
,则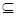 M
M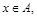 则
则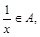 就称A是伙伴关系集合,集合
就称A是伙伴关系集合,集合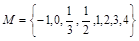 的所有非空子集中,具有伙伴关系的集合的个数为
的所有非空子集中,具有伙伴关系的集合的个数为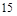
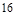
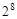
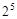
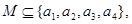
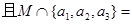

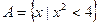 ,
,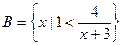
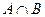 ;(2)若不等式
;(2)若不等式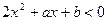 的解集为
的解集为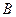 ,求
,求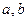 的值
的值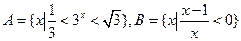 ,则
,则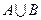 ="___________."
="___________."