题目内容
数列{an}满足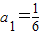 ,前n项和
,前n项和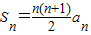
(1)写出a2,a3,a4;
(2)猜出an的表达式,并用数学归纳法证明.
【答案】分析:(1)根据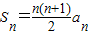 ,利用递推公式,分别令n=2,3,4.求出a1,a2,a3,a4;
,利用递推公式,分别令n=2,3,4.求出a1,a2,a3,a4;
(2)根据(1)求出的数列的前四项,从而总结出规律猜出an,然后利用数学归纳法进行证明即得.
解答:解:(1)令n=2,∵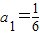 ,∴
,∴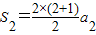 ,即a1+a2=3a2.∴
,即a1+a2=3a2.∴ .
.
令n=3,得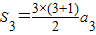 ,即a1+a2+a3=6a3,∴
,即a1+a2+a3=6a3,∴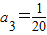 .
.
令n=4,得 ,a1+a2+a3+a4=10a4,∴
,a1+a2+a3+a4=10a4,∴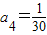 .
.
(2)猜想 ,下面用数学归纳法给出证明.
,下面用数学归纳法给出证明.
①当n=1时,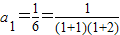 结论成立.
结论成立.
②假设当n=k时,结论成立,即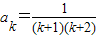 ,
,
则当n=k+1时,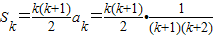
=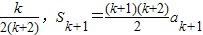 ,
,
即 .
.
∴
∴ .
.
∴当n=k+1时结论成立.
由①②可知,对一切n∈N+都有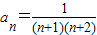 成立.
成立.
点评:此题主要考查数列递推式、数学归纳法.数学归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而求证.
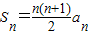 ,利用递推公式,分别令n=2,3,4.求出a1,a2,a3,a4;
,利用递推公式,分别令n=2,3,4.求出a1,a2,a3,a4;(2)根据(1)求出的数列的前四项,从而总结出规律猜出an,然后利用数学归纳法进行证明即得.
解答:解:(1)令n=2,∵
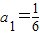 ,∴
,∴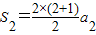 ,即a1+a2=3a2.∴
,即a1+a2=3a2.∴ .
.令n=3,得
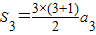 ,即a1+a2+a3=6a3,∴
,即a1+a2+a3=6a3,∴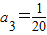 .
.令n=4,得
 ,a1+a2+a3+a4=10a4,∴
,a1+a2+a3+a4=10a4,∴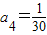 .
.(2)猜想
 ,下面用数学归纳法给出证明.
,下面用数学归纳法给出证明.①当n=1时,
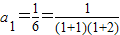 结论成立.
结论成立.②假设当n=k时,结论成立,即
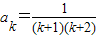 ,
,则当n=k+1时,
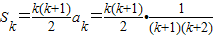
=
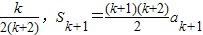 ,
,即
 .
.∴

∴
 .
.∴当n=k+1时结论成立.
由①②可知,对一切n∈N+都有
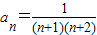 成立.
成立.点评:此题主要考查数列递推式、数学归纳法.数学归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而求证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
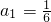 ,前n项和
,前n项和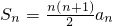
 ,前n项和为Sn,若Sn=340,求n的值.
,前n项和为Sn,若Sn=340,求n的值.