题目内容
函数f(x)=x3+ax2+bx+c,x∈[-2,2],表示的曲线过原点,且在x=±1处的切线的斜率均为-1,有以下命题:①f(x)的解析式是f(x)=x3-4x,x∈[-2,2];
②f(x)的极值点有且只有1个;
③f(x)的最大值与最小值之和为0;
其中真命题的序号是 .
【答案】分析:首先利用导数的几何意义及函数f(x)过原点,列方程组求出f(x)的解析式;然后根据奇函数的定义判断函数f(x)的奇偶性,且由f′(x)的最小值求出k的最大值,则命题①④得出判断;最后令f′(x)=0,求出f(x)的极值点,进而求得f(x)的单调区间与最值,则命题②③得出判断.
解答:解:函数f(x)=x3+ax2+bx+c的图象过原点,可得c=0;
又f′(x)=3x2+2ax+b,且f(x)在x=±1处的切线斜率均为-1,
则有 ,解得a=0,b=-4.
,解得a=0,b=-4.
所以f(x)=x3-4x,f′(x)=3x2-4.
①可见f(x)=x3-4x,因此①正确;
②令f′(x)=0,得x=±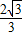 .因此②不正确;
.因此②不正确;
所以f(x)在[-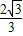 ,
,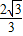 ]内递减,
]内递减,
且f(x)的极大值为f(-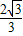 )=
)=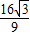 ,极小值为f(
,极小值为f( 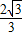 )=-
)=-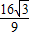 ,两端点处f(-2)=f(2)=0,
,两端点处f(-2)=f(2)=0,
所以f(x)的最大值为M=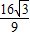 ,最小值为m=-
,最小值为m=-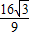 ,则M+m=0,因此③正确.
,则M+m=0,因此③正确.
故答案为:①③.
点评:本题主要考查导数的几何意义及利用导数研究函数单调性、最值的方法.
解答:解:函数f(x)=x3+ax2+bx+c的图象过原点,可得c=0;
又f′(x)=3x2+2ax+b,且f(x)在x=±1处的切线斜率均为-1,
则有
 ,解得a=0,b=-4.
,解得a=0,b=-4.所以f(x)=x3-4x,f′(x)=3x2-4.
①可见f(x)=x3-4x,因此①正确;
②令f′(x)=0,得x=±
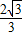 .因此②不正确;
.因此②不正确;所以f(x)在[-
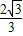 ,
,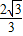 ]内递减,
]内递减,且f(x)的极大值为f(-
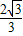 )=
)=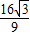 ,极小值为f(
,极小值为f( 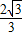 )=-
)=-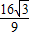 ,两端点处f(-2)=f(2)=0,
,两端点处f(-2)=f(2)=0,所以f(x)的最大值为M=
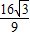 ,最小值为m=-
,最小值为m=-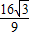 ,则M+m=0,因此③正确.
,则M+m=0,因此③正确.故答案为:①③.
点评:本题主要考查导数的几何意义及利用导数研究函数单调性、最值的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目