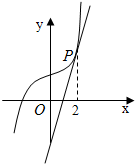题目内容
f(x)=ax3+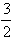 bx2(a≠0,a,b∈R)的图象在点(2,f(2))处的切线与x轴平行。
bx2(a≠0,a,b∈R)的图象在点(2,f(2))处的切线与x轴平行。
(1)求函数f(x)的单调递减区间;
(2)若已知a>b,求函数f(x)在[b,a]上的最大值。
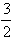 bx2(a≠0,a,b∈R)的图象在点(2,f(2))处的切线与x轴平行。
bx2(a≠0,a,b∈R)的图象在点(2,f(2))处的切线与x轴平行。(1)求函数f(x)的单调递减区间;
(2)若已知a>b,求函数f(x)在[b,a]上的最大值。
解:(1)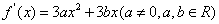
由题意知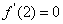
∴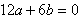
整理得b=-2a
∴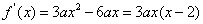
当a>0时,由f'(x)<0,得0<x<2,
∴f(x)的单调递减区间为(0,2);
当a<0时,由f'(x)<0,得x<0或x>2
∴f(x)的单调递减区间为(-∞,0)和(2,+∞)。
(2)∵a>b且b=-2a,
∴a>0,b<0
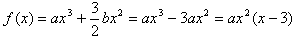
由f(x)=0得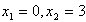
①当0<a≤3时,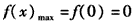
②当a>3时,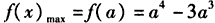
综上所述:当0<a≤3时,f (x)的最大值为0;当a>3时,f(x)的最大值为a4-3a3。
由题意知
∴
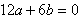
整理得b=-2a
∴
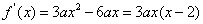
当a>0时,由f'(x)<0,得0<x<2,
∴f(x)的单调递减区间为(0,2);
当a<0时,由f'(x)<0,得x<0或x>2
∴f(x)的单调递减区间为(-∞,0)和(2,+∞)。
(2)∵a>b且b=-2a,
∴a>0,b<0
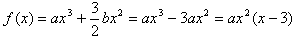
由f(x)=0得
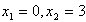
①当0<a≤3时,
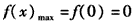
②当a>3时,
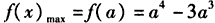
综上所述:当0<a≤3时,f (x)的最大值为0;当a>3时,f(x)的最大值为a4-3a3。

练习册系列答案
相关题目
 已知函数f(x)=ax3+b,其图象在点P处的切线为l:y=4x-4,点P的横坐标为2(如图).求直线l、直线x=0、直线y=0以及f(x)的图象在第一象限所围成区域的面积.
已知函数f(x)=ax3+b,其图象在点P处的切线为l:y=4x-4,点P的横坐标为2(如图).求直线l、直线x=0、直线y=0以及f(x)的图象在第一象限所围成区域的面积. 已知函数f(x)=ax3+b,其图象在点P处的切线为l:y=4x-4,点P的横坐标为2(如图).求直线l、直线x=0、直线y=0以及f(x)的图象在第一象限所围成区域的面积.
已知函数f(x)=ax3+b,其图象在点P处的切线为l:y=4x-4,点P的横坐标为2(如图).求直线l、直线x=0、直线y=0以及f(x)的图象在第一象限所围成区域的面积.