题目内容
若P两条异面直线l,m外的任意一点,则( )
| A.过点P有且仅有一条直线与l,m都平行 |
| B.过点P有且仅有一条直线与l,m都垂直 |
| C.过点P有且仅有一条直线与l,m都相交 |
| D.过点P有且仅有一条直线与l,m都异面 |
设过点P的直线为n,若n与l、m都平行,则l、m平行,与l、m异面矛盾,故选项A错误;
由于l、m只有唯一的公垂线,而过点P与公垂线平行的直线只有一条,故B正确;
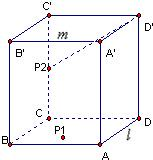
对于选项C、D可参考下图的正方体,设AD为直线l,A′B′为直线m,若点P在P1点,则显然无法作出直线与两直线都相交,故选项C错误;若P在P2点,则由图中可知直线CC′及D′P2均与l、m异面,故选项D错误.
故选B.
由于l、m只有唯一的公垂线,而过点P与公垂线平行的直线只有一条,故B正确;
对于选项C、D可参考下图的正方体,设AD为直线l,A′B′为直线m,若点P在P1点,则显然无法作出直线与两直线都相交,故选项C错误;若P在P2点,则由图中可知直线CC′及D′P2均与l、m异面,故选项D错误.

故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目