题目内容
已知{an}是公差为d的等差数列,{bn}是公比为q的等比数列,
(1)若an=3n+1,是否存在m,n∈N*,有am+am+1=ak?请说明理由;
(2)若bn=aqn(a、q为常数,且aq≠0)对任意m存在k,有bm·bm+1=bk,试求a、q满足的充要条件;
(3)若an=2n+1,bn=3n,试确定所有的p,使数列{bn}中存在某个连续p项的和式数列中{an}的一项,请证明。
(1)若an=3n+1,是否存在m,n∈N*,有am+am+1=ak?请说明理由;
(2)若bn=aqn(a、q为常数,且aq≠0)对任意m存在k,有bm·bm+1=bk,试求a、q满足的充要条件;
(3)若an=2n+1,bn=3n,试确定所有的p,使数列{bn}中存在某个连续p项的和式数列中{an}的一项,请证明。
解:(1)由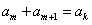 ,得6m+5=3k+1,
,得6m+5=3k+1,
整理后,可得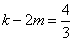 ,
,
∵m、k∈N,
∴k-2m为整数
∴不存在n、k∈N*,使等式成立。
(2)当m=1时,则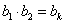 ,
,
∴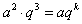 ,
,
∴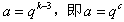 ,其中c是大于等于-2的整数,
,其中c是大于等于-2的整数,
反之当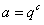 时,其中c是大于等于-2的整数,则
时,其中c是大于等于-2的整数,则 ,
,
显然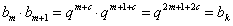 ,其中k=2m+1+c,
,其中k=2m+1+c,
∴a、q满足的充要条件是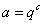 ,其中c是大于等于-2的整数。
,其中c是大于等于-2的整数。
(3)设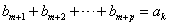 ,
,
当p为偶数时,(*)式左边为偶数,右边为奇数;
当p为偶数时,(*)式不成立。
由(*)式得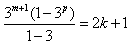 ,整理得
,整理得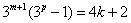 ,
,
当p=1时,符合题意;
当p≥3,p为奇数时,
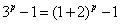
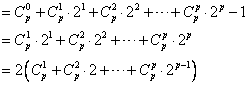
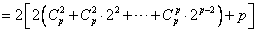 ,
,
∴由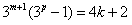 ,
,
得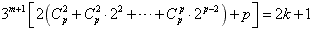 ,
,
∴当p为奇数时,此时,一定有m和k使上式一定成立;
∴当p为奇数时,命题都成立。
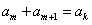 ,得6m+5=3k+1,
,得6m+5=3k+1,整理后,可得
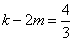 ,
, ∵m、k∈N,
∴k-2m为整数
∴不存在n、k∈N*,使等式成立。
(2)当m=1时,则
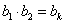 ,
,∴
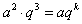 ,
, ∴
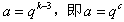 ,其中c是大于等于-2的整数,
,其中c是大于等于-2的整数,反之当
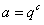 时,其中c是大于等于-2的整数,则
时,其中c是大于等于-2的整数,则 ,
,显然
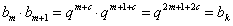 ,其中k=2m+1+c,
,其中k=2m+1+c,∴a、q满足的充要条件是
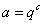 ,其中c是大于等于-2的整数。
,其中c是大于等于-2的整数。(3)设
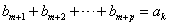 ,
,当p为偶数时,(*)式左边为偶数,右边为奇数;
当p为偶数时,(*)式不成立。
由(*)式得
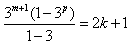 ,整理得
,整理得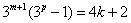 ,
,当p=1时,符合题意;
当p≥3,p为奇数时,
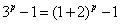
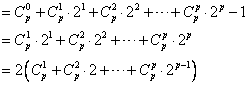
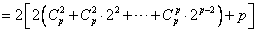 ,
,∴由
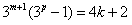 ,
,得
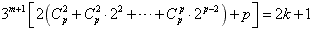 ,
,∴当p为奇数时,此时,一定有m和k使上式一定成立;
∴当p为奇数时,命题都成立。

练习册系列答案
相关题目