题目内容
已知:命题p:函数g(x)的图象与函数f(x)=1-3x的图象关于直线y=x对称,且|g(a)|<2.命题q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0},且A∩B=φ.求实数a的取值范围,使命题p、q有且只有一个是真命题.
【答案】分析:据关于y=x对称的两个函数互为反函数求出g(x),解绝对值不等式求出命题p为真命题时a的范围,根据两集合的交集为∅时,对集合A分类讨论:A=∅时,△<0;A≠∅时,即方程的根为非正根求出q为真命题时a的范围;命题p、q有且只有一个是真命题,分类讨论求出a的范围.
解答:解:若命题p是真命题则有
因为f(x)=1-3x,所以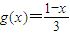
由|g(a)|<2,得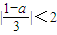 ,解得-5<a<7
,解得-5<a<7
若命题q为真命题则有
∵A∩B=φ,且B={x|x>0},故集合A应分为A=φ和A≠φ两种情况
当A=φ时,△=(a+2)2-4<0,解得-4<a<0
当A≠φ时,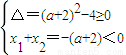
解得a≥0
故a>-4
若p真q假,则-5<a≤4,
若p假q真,则a≥7
使命题p、q有且只有一个是真命题实数a的取值范围为(-5,4]∪[7,+∞),
点评:本题考查复合命题的真假与组成其简单命题的真假的关系.
解答:解:若命题p是真命题则有
因为f(x)=1-3x,所以
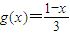
由|g(a)|<2,得
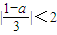 ,解得-5<a<7
,解得-5<a<7若命题q为真命题则有
∵A∩B=φ,且B={x|x>0},故集合A应分为A=φ和A≠φ两种情况
当A=φ时,△=(a+2)2-4<0,解得-4<a<0
当A≠φ时,
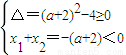
解得a≥0
故a>-4
若p真q假,则-5<a≤4,
若p假q真,则a≥7
使命题p、q有且只有一个是真命题实数a的取值范围为(-5,4]∪[7,+∞),
点评:本题考查复合命题的真假与组成其简单命题的真假的关系.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目