题目内容
(本小题满分12分)
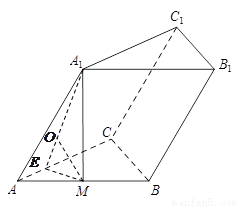
已知斜三棱柱ABC—A1B1C1的底面是正三角形,侧面ABB1A1是边长为2的菱形,且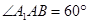 ,M是AB的中点,
,M是AB的中点,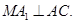

(1)求证: 平面ABC;
平面ABC;
(2)求点M到平面AA1C1C的距离.
【答案】
(1)见解析;
(2)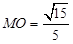
【解析】(1)因为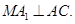 ,只需证
,只需证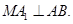 即可.然后证
即可.然后证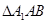 为正三角形.
为正三角形.
(2)在(1)的基础上,取AC的中点N,连接A1N,则易证: ,
,
所以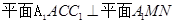 ,再过M作
,再过M作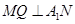 ,垂直为Q,则MQ为点M到平面AA1C1C的距离.
,垂直为Q,则MQ为点M到平面AA1C1C的距离.
(Ⅰ)∵侧面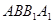 是菱形,
是菱形,
且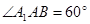 ,∴
,∴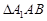 为正三角形.
为正三角形.
又∵点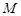 为
为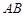 的中点,∴
的中点,∴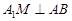 ,
,
由已知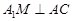 ,∴
,∴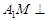 平面
平面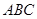 .(4分)
.(4分)
(Ⅱ)作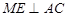 于
于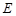 , 连接
, 连接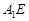 ,作
,作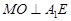 于
于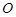 ,
,
由已知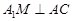 , 又∵
, 又∵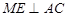 ,∴
,∴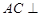 面
面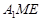 ,
,
由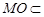 面
面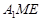 , 得
, 得 ,
,
∵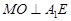 ,且
,且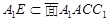 ,
, 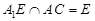 ,∴
,∴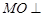 面
面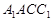 ,
,
于是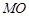 即为所求,
(8分)
即为所求,
(8分)
∵菱形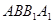 边长为2,易得
边长为2,易得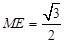 ,
, 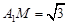 ,
,
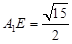 ,
,
∴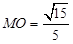 .
(12分)
.
(12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目