题目内容
设 是非零向量,已知命题P:若
是非零向量,已知命题P:若 ,
, ,则
,则 ;命题q:若
;命题q:若 ,则
,则 ,则下列命题中真命题是( )
,则下列命题中真命题是( )
A. | B. | C. | D. |
A
解析试题分析:由题意可知,命题P是假命题;命题q是真命题,故 为真命题.
为真命题.
考点:命题的真假.

练习册系列答案
相关题目
下列说法正确的是( ).
A.命题“若 ,则 ,则 ”的逆命题是“若 ”的逆命题是“若 ,则 ,则 ” ” |
B.命题“若 ,则 ,则 ”的否命题是“若 ”的否命题是“若 ,则 ,则 ” ” |
C.已知 ,则“ ,则“ ”是“ ”是“ ”的充要条件 ”的充要条件 |
D.已知 ,则“ ,则“ ”是“ ”是“ ”的充分条件 ”的充分条件 |
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数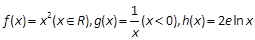 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
函数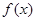 在
在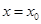 处导数存在,若
处导数存在,若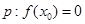 ;
;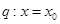 是
是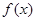 的极值点,则( )
的极值点,则( )
A.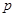 是 是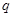 的充分必要条件 的充分必要条件 |
B.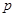 是 是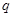 的充分条件,但不是 的充分条件,但不是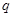 的必要条件 的必要条件 |
C.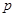 是 是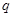 的必要条件,但不是 的必要条件,但不是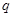 的充分条件 的充分条件 |
D.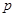 既不是 既不是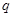 的充分条件,也不是 的充分条件,也不是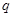 的必要条件 的必要条件 |
设 ,集合
,集合 是奇数集,集合
是奇数集,集合 是偶数集.若命题
是偶数集.若命题 ,则( )
,则( )
A.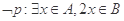 | B. |
C. | D. |
设条件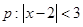 , 条件
, 条件 , 其中
, 其中 为正常数.若
为正常数.若 是
是 的必要不充分条件,则
的必要不充分条件,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.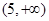 |
下列判断错误的是( )
A.“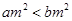 ”是“ ”是“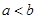 ”的充分不必要条件 ”的充分不必要条件 |
B.“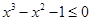 对 对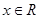 恒成立”的否定是“存在 恒成立”的否定是“存在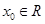 使得 使得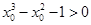 ” ” |
C.若“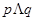 ”为假命题,则 ”为假命题,则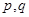 均为假命题 均为假命题 |
D.若随机变量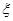 服从二项分布: 服从二项分布: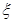 ~ ~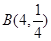 ,则 ,则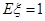 |
已知命题p:对?x∈R,?m∈R,使4x+2xm+1=0.若命题 p是假命题,则实数m的取值范围是( )
p是假命题,则实数m的取值范围是( )
| A.[-2,2] | B.[2,+∞) |
| C.(-∞,-2] | D.[-2,+∞) |
“不等式x2-x+m>0在R上恒成立”的一个必要不充分条件是( )
A.m>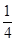 | B.0<m<1 |
| C.m>0 | D.m>1 |