题目内容
已知函数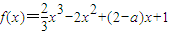 ,其中a∈R.
,其中a∈R.(Ⅰ)若a=2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)在区间[2,3]上的最大值和最小值.
【答案】分析:(Ⅰ)求导数,把a=2代入可得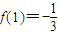 ,f'(1)=-2,由点斜式可写直线的方程,化为一般式即可;
,f'(1)=-2,由点斜式可写直线的方程,化为一般式即可;
(Ⅱ)由△=8a,分a≤0,当a>0两大类来判断,其中当a>0时,又需分0<a≤2,2<a<8,a≥8,三种情形来判断,综合可得答案.
解答:(Ⅰ)解:f(x)的定义域为R,且 f'(x)=2x2-4x+2-a,当a=2时,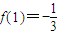 ,f'(1)=-2,
,f'(1)=-2,
所以曲线y=f(x)在点(1,f(1))处的切线方程为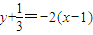 ,即 6x+3y-5=0.(4分)
,即 6x+3y-5=0.(4分)
(Ⅱ)解:方程f'(x)=0的判别式为△=(-4)2-4×2×(2-a)=8a.
(ⅰ)当a≤0时,f'(x)≥0,所以f(x)在区间(2,3)上单调递增,所以f(x)在区间[2,3]
上的最小值是 ;最大值是f(3)=7-3a.
;最大值是f(3)=7-3a.
(ⅱ)当a>0时,令f'(x)=0,得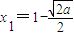 ,或
,或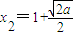 .f(x)和f'(x)的情况如下:
.f(x)和f'(x)的情况如下:
故f(x)的单调增区间为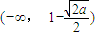 ,
,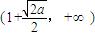 ;单调减区间为
;单调减区间为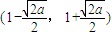 .
.
①当0<a≤2时,x2≤2,此时f(x)在区间(2,3)上单调递增,所以f(x)在区间[2,3]
上的最小值是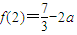 ;最大值是f(3)=7-3a.
;最大值是f(3)=7-3a.
②当2<a<8时,x1<2<x2<3,此时f(x)在区间(2,x2)上单调递减,在区间(x2,3)上单调递增,
所以f(x)在区间[2,3]上的最小值是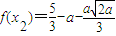 .
.
因为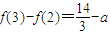 ,
,
所以 当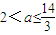 时,f(x)在区间[2,3]上的最大值是f(3)=7-3a;当
时,f(x)在区间[2,3]上的最大值是f(3)=7-3a;当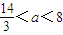 时,f(x)在区间[2,3]上的最大值是
时,f(x)在区间[2,3]上的最大值是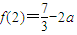 .
.
③当a≥8时,x1<2<3≤x2,此时f(x)在区间(2,3)上单调递减,
所以f(x)在区间[2,3]上的最小值是f(3)=7-3a;最大值是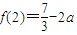 .
.
综上可得,
当a≤2时,f(x)在区间[2,3]上的最小值是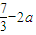 ,最大值是7-3a;
,最大值是7-3a;
当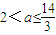 时,f(x)在区间[2,3]上的最小值是
时,f(x)在区间[2,3]上的最小值是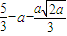 ,最大值是7-3a;
,最大值是7-3a;
当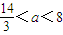 时,f(x)在区间[2,3]上的最小值是
时,f(x)在区间[2,3]上的最小值是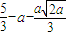 ,最大值是
,最大值是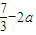 ;
;
当a≥8时,f(x)在区间[2,3]上的最小值是7-3a,最大值是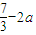 .
.
点评:本题考查利用导数研究函数的单调性和最值问题,涉及切线方程问题,属中档题.
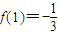 ,f'(1)=-2,由点斜式可写直线的方程,化为一般式即可;
,f'(1)=-2,由点斜式可写直线的方程,化为一般式即可;(Ⅱ)由△=8a,分a≤0,当a>0两大类来判断,其中当a>0时,又需分0<a≤2,2<a<8,a≥8,三种情形来判断,综合可得答案.
解答:(Ⅰ)解:f(x)的定义域为R,且 f'(x)=2x2-4x+2-a,当a=2时,
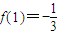 ,f'(1)=-2,
,f'(1)=-2,所以曲线y=f(x)在点(1,f(1))处的切线方程为
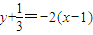 ,即 6x+3y-5=0.(4分)
,即 6x+3y-5=0.(4分)(Ⅱ)解:方程f'(x)=0的判别式为△=(-4)2-4×2×(2-a)=8a.
(ⅰ)当a≤0时,f'(x)≥0,所以f(x)在区间(2,3)上单调递增,所以f(x)在区间[2,3]
上的最小值是
 ;最大值是f(3)=7-3a.
;最大值是f(3)=7-3a.(ⅱ)当a>0时,令f'(x)=0,得
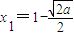 ,或
,或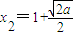 .f(x)和f'(x)的情况如下:
.f(x)和f'(x)的情况如下:| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f'(x) | + | - | + | ||
| f(x) | ↗ | ↘ | ↗ |
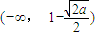 ,
,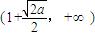 ;单调减区间为
;单调减区间为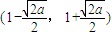 .
.①当0<a≤2时,x2≤2,此时f(x)在区间(2,3)上单调递增,所以f(x)在区间[2,3]
上的最小值是
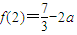 ;最大值是f(3)=7-3a.
;最大值是f(3)=7-3a.②当2<a<8时,x1<2<x2<3,此时f(x)在区间(2,x2)上单调递减,在区间(x2,3)上单调递增,
所以f(x)在区间[2,3]上的最小值是
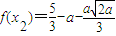 .
.因为
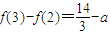 ,
,所以 当
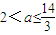 时,f(x)在区间[2,3]上的最大值是f(3)=7-3a;当
时,f(x)在区间[2,3]上的最大值是f(3)=7-3a;当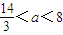 时,f(x)在区间[2,3]上的最大值是
时,f(x)在区间[2,3]上的最大值是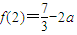 .
.③当a≥8时,x1<2<3≤x2,此时f(x)在区间(2,3)上单调递减,
所以f(x)在区间[2,3]上的最小值是f(3)=7-3a;最大值是
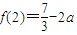 .
.综上可得,
当a≤2时,f(x)在区间[2,3]上的最小值是
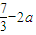 ,最大值是7-3a;
,最大值是7-3a;当
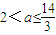 时,f(x)在区间[2,3]上的最小值是
时,f(x)在区间[2,3]上的最小值是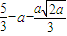 ,最大值是7-3a;
,最大值是7-3a;当
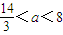 时,f(x)在区间[2,3]上的最小值是
时,f(x)在区间[2,3]上的最小值是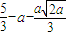 ,最大值是
,最大值是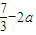 ;
;当a≥8时,f(x)在区间[2,3]上的最小值是7-3a,最大值是
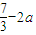 .
.点评:本题考查利用导数研究函数的单调性和最值问题,涉及切线方程问题,属中档题.

练习册系列答案
相关题目
 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.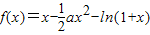 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.