题目内容
若椭圆C: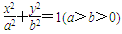 的离心率e为
的离心率e为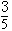 , 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.
, 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.
(1) 求椭圆C的方程;
(2) 设点M(2,0), 点Q是椭圆上一点, 当|MQ|最小时, 试求点Q的坐标;
(3) 设P(m,0)为椭圆C长轴(含端点)上的一个动点, 过P点斜率为k的直线l交椭圆与
A,B两点, 若|PA|2+|PB|2的值仅依赖于k而与m无关, 求k的值.
【答案】
(1)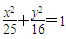
(2)(5,0)
(3)k=± .
.
【解析】
试题分析:解:(1)∵依题意a=5,c=3∴椭圆C的方程为: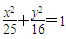 2¢
2¢
(2)设Q(x,y), -5≤x≤5
∴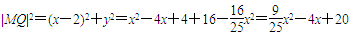
∵对称轴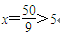
∴当x=5时, |MQ|2达到最小值,
∴当|MQ|最小时, Q的坐标为(5,0) ·6¢
(3)设A(x1,y1), B(x2,y2), P(m,0)(-5≤m≤5), 直线l:y=k(x-m)
由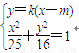
得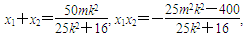 ,
8¢
,
8¢
∴y1+y2=k(x1-m)+k(x2-m)=k(x1+x2)-2km=
y1y2=k2(x1-m)(x2-m)=k2x1x2-k2m(x1+x2)+k2m2=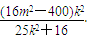 ·
10¢
·
10¢
∴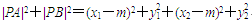
=(x1+x2)2-2x1x2-2a(x1+x2)+(y1+y2)2-2y1y2-2y1y2+2a2
=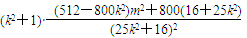 -12分
-12分
∵|PA|2+|PB|2的值仅依赖于k而与m无关
∴512-800k2=0∴k=± .
13¢
.
13¢
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的运用,属于中档题。

练习册系列答案
相关题目
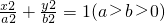 的离心率e为
的离心率e为 ,且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.
,且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.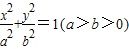 的离心率e=
的离心率e= ,且过点P(1,
,且过点P(1, ).
).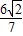 ,求l的方程.
,求l的方程. 若椭圆C:
若椭圆C: