题目内容
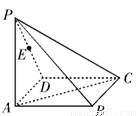
如图,在四棱锥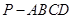 中,底面
中,底面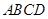 为矩形,侧棱
为矩形,侧棱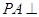 底面
底面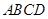 ,
,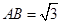 ,
,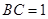 ,
, ,
,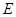 为
为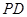 的中点.
的中点.
(1)求直线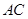 与
与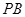 所成角的余弦值;
所成角的余弦值;
(2)在侧面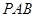 内找一点
内找一点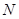 ,使
,使 面
面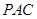 ,并求出
,并求出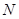 点到直线
点到直线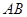 和
和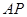 的距离.
的距离.
【答案】
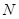 点的坐标为
点的坐标为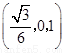 ,从而
,从而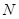 点到
点到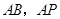 的距离分别为
的距离分别为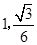 .
.
【解析】
试题分析:解:(1)建立如图所示的空间直角坐标系,
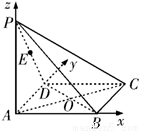
则 的坐标为
的坐标为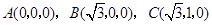 ,
,
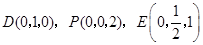 ,
,
从而 .
.
设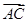 与
与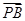 的夹角为
的夹角为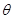 ,
,
则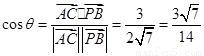 ,
,
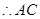 与
与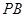 所成角的余弦值为
所成角的余弦值为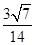 ;
;
(2)由于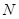 点在侧面
点在侧面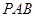 内,故可设
内,故可设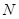 点坐标为
点坐标为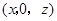 ,
,
则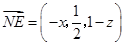 ,
,
由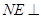 面
面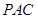 ,可得
,可得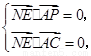
即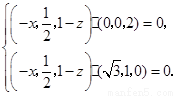
化简,得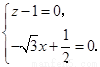
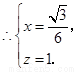
即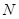 点的坐标为
点的坐标为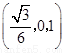 ,从而
,从而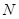 点到
点到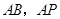 的距离分别为
的距离分别为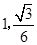 .
.
考点:本题主要考查空间向量的应用,向量的数量积,向量的坐标运算。
点评:典型综合题。通过建立空间直角坐标系,将求异面直线的夹角余弦及距离计算问题,转化成向量的坐标运算。

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小. 中,底面
中,底面 是菱形,
是菱形, ,
, ,
, ,
, 平面
平面 是
是 的中点,
的中点, 是
是 的中点.
的中点.  ∥平面
∥平面 ;
; ;
; 所成的锐二面角的大小.
所成的锐二面角的大小.
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
. 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小.
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, 为
为 中点,作
中点,作 交
交 于
于

 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。 中,底面
中,底面 为平行四边形,
为平行四边形, 平面
平面

 在棱
在棱 上.
上.
 时,求证
时,求证 平面
平面
 的大小为
的大小为 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.