题目内容
对某电子元件进行寿命追踪调查,情况如表:| 寿命/小时 | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
| 分组 | 频数 | 频率 |
| 100~200 | ||
| 200~300 | ||
| 300~400 | ||
| 400~500 | ||
| 500~600 | ||
| 合计 |
(3)在上述追踪调查的电子元件中任取2个,设ξ为其中寿命在400~500小时的电子元件个数,求ξ的分布列.
分析:(1)根据所给的表格,填入频率分布表中的频数,用频数除以样本容量,得到要求的频率,填入表中.
(2)根据所给的频率分布表,画出频率分步直方图,做出频率分步直方图是解题的关键.
(3)追踪调查的电子元件总数为200个,其中寿命在400~500小时的有40个,ξ的可能取值为0,1,2,结合变量对应的事件写出变量的概率和分布列.
(2)根据所给的频率分布表,画出频率分步直方图,做出频率分步直方图是解题的关键.
(3)追踪调查的电子元件总数为200个,其中寿命在400~500小时的有40个,ξ的可能取值为0,1,2,结合变量对应的事件写出变量的概率和分布列.
解答:解:(1)完成频率分布表如表:
(2)完成频率分布直方图如图
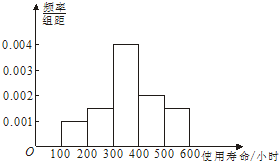
(3)由题意,得追踪调查的电子元件总数为200个,其中寿命在400~500小时的有40个,
ξ的可能取值为0,1,2.
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
∴ξ的分布列为
| 分组 | 频数 | 频率 |
| 100~200 | 20 | 0.10 |
| 200~300 | 30 | 0.15 |
| 300~400 | 80 | 0.40 |
| 400~500 | 40 | 0.20 |
| 500~600 | 30 | 0.15 |
| 合计 | 200 | 1 |

(3)由题意,得追踪调查的电子元件总数为200个,其中寿命在400~500小时的有40个,
ξ的可能取值为0,1,2.
P(ξ=0)=
| ||
|
| 636 |
| 995 |
P(ξ=1)=
| ||||
|
| 64 |
| 199 |
P(ξ=2)=
| ||
|
| 39 |
| 995 |
∴ξ的分布列为
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
点评:本题考查频率分布表和频率分步直方图,考查离散型随机变量的分布列,本题是一个概率与统计的综合题目,可以作为一个高考题目出现.

练习册系列答案
相关题目

 对某电子元件进行寿命追踪调查,情况如下:
对某电子元件进行寿命追踪调查,情况如下: