题目内容
已知椭圆C: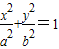 (a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为
(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)已知一直线l过椭圆C的右焦点F2,交椭圆于点A、B.
(ⅰ)若满足
 (O为坐标原点),求△AOB的面积;
(O为坐标原点),求△AOB的面积;(ⅱ)当直线l与两坐标轴都不垂直时,在x轴上是否总存在一点P,使得直线PA、PB的倾斜角互为补角?若存在,求出P坐标;若不存在,请说明理由.
【答案】分析:(Ⅰ)由焦点坐标得出c=1,结合离心率得出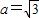 ,求出b 值,最后写出椭圆C的方程即可;
,求出b 值,最后写出椭圆C的方程即可;
(II)(i)由题中条件:“ ”结合向量的数量积,代入三角形面积公式求得答案.
”结合向量的数量积,代入三角形面积公式求得答案.
(ii)对于存在性问题,可先假设存在,即假设存在一点P,使得直线PA、PB的倾斜角互为补角,再利用方程的思想,求出m的值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(Ⅰ)c=1,又 ,∴
,∴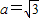
∴b2=a2-c2=3-1=2
所以,椭圆C的方程是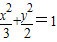
(Ⅱ)(ⅰ)∵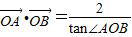 ,∴
,∴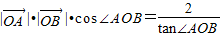 ,
,
∴ ,∴
,∴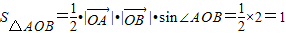 .
.
(ⅱ)假设存在一点P,使得直线PA、PB的倾斜角互为补角,
依题意可知直线l、PA、PB斜率存在且不为零.
不妨设P(m,0),直线l的方程为y=k(x-1),k≠0
由 消去y得(3k2+2)x2-6k2x+3k2-6=0
消去y得(3k2+2)x2-6k2x+3k2-6=0
设A(x1,y1),B(x2,y2)则
∵直线PA、PB的倾斜角互为补角,
∴kPA+kPB=0对一切k恒成立,即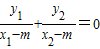 对一切k恒成立
对一切k恒成立
又y1=k(x1-1),y2=k(x2-1),
代入上式可得2x1x2+2m-(m+1)(x1+x2)=0对一切k恒成立
∴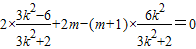 对一切k恒成立,
对一切k恒成立,
即2m-6=0,∴m=3,
∴存在P(3,0)使得直线PA、PB的倾斜角互为补角.
点评:本小题考查椭圆的几何性质、直线与椭圆等基础知识,同时考查解析几何的基本思想方法和综合解题能力;注意(Ⅲ)的处理存在性问题的一般方法,首先假设存在,进而根据题意、结合有关性质,化简、转化、计算,最后得到结论.
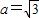 ,求出b 值,最后写出椭圆C的方程即可;
,求出b 值,最后写出椭圆C的方程即可;(II)(i)由题中条件:“
 ”结合向量的数量积,代入三角形面积公式求得答案.
”结合向量的数量积,代入三角形面积公式求得答案.(ii)对于存在性问题,可先假设存在,即假设存在一点P,使得直线PA、PB的倾斜角互为补角,再利用方程的思想,求出m的值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(Ⅰ)c=1,又
 ,∴
,∴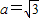
∴b2=a2-c2=3-1=2
所以,椭圆C的方程是
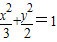
(Ⅱ)(ⅰ)∵
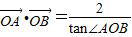 ,∴
,∴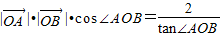 ,
,∴
 ,∴
,∴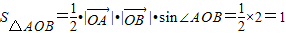 .
.(ⅱ)假设存在一点P,使得直线PA、PB的倾斜角互为补角,
依题意可知直线l、PA、PB斜率存在且不为零.
不妨设P(m,0),直线l的方程为y=k(x-1),k≠0
由
 消去y得(3k2+2)x2-6k2x+3k2-6=0
消去y得(3k2+2)x2-6k2x+3k2-6=0设A(x1,y1),B(x2,y2)则

∵直线PA、PB的倾斜角互为补角,
∴kPA+kPB=0对一切k恒成立,即
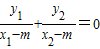 对一切k恒成立
对一切k恒成立又y1=k(x1-1),y2=k(x2-1),
代入上式可得2x1x2+2m-(m+1)(x1+x2)=0对一切k恒成立
∴
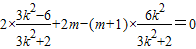 对一切k恒成立,
对一切k恒成立,即2m-6=0,∴m=3,
∴存在P(3,0)使得直线PA、PB的倾斜角互为补角.
点评:本小题考查椭圆的几何性质、直线与椭圆等基础知识,同时考查解析几何的基本思想方法和综合解题能力;注意(Ⅲ)的处理存在性问题的一般方法,首先假设存在,进而根据题意、结合有关性质,化简、转化、计算,最后得到结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。