题目内容
函数f(x)=x3+ax2+bx-2的图象在与y轴交点的切线方程为y=x+a.(1)求函数f(x)的解析式;
(2)设函数
 存在极值,求实数m的取值范围.
存在极值,求实数m的取值范围.
【答案】分析:(1)利用切点为(0,-2)和f′(0)=1可得a,b,进而求出函数的解析式.
(2)转化为g′(x)=0有实根.根据判别式求出对应的根,再找函数的极值即可.
解答:解:(1)由已知可得切点为(0,-2),所以a=-2,
又因为f′(x)=3x2+2ax+b,
所以f′(0)=b=1.
所以函数解析式为f(x)=x3-2x2+x-2.
(2)由(1)可得:g(x)=x3-2x2+x-2+ mx,
mx,
所以g′(x)=3x2-4x+1+ ,令g′(x)=0.
,令g′(x)=0.
当函数有极值时,方程3x2-4x+1+ =0有实根,即△≥0,
=0有实根,即△≥0,
由△=4(1-m)≥0,得m≤1.
①当m=1时,g′(x)=0有实根x= ,在x=
,在x= 左右两侧均有g′(x)>0,故函数g(x)无极值.
左右两侧均有g′(x)>0,故函数g(x)无极值.
②当m<1时,g′(x)=0有两个实根,
x1= (2-
(2-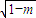 ),x2=
),x2= (2+
(2+ ),
),
当x变化时,g′(x)、g(x)的变化情况如下表:
故在m∈(-∞,1)时,函数g(x)有极值;当x= (2-
(2- )时,g(x)有极大值;当x=
)时,g(x)有极大值;当x= (2+
(2+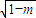 ) 时,g(x)有极小值.
) 时,g(x)有极小值.
点评:本题考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.
(2)转化为g′(x)=0有实根.根据判别式求出对应的根,再找函数的极值即可.
解答:解:(1)由已知可得切点为(0,-2),所以a=-2,
又因为f′(x)=3x2+2ax+b,
所以f′(0)=b=1.
所以函数解析式为f(x)=x3-2x2+x-2.
(2)由(1)可得:g(x)=x3-2x2+x-2+
 mx,
mx,所以g′(x)=3x2-4x+1+
 ,令g′(x)=0.
,令g′(x)=0.当函数有极值时,方程3x2-4x+1+
 =0有实根,即△≥0,
=0有实根,即△≥0,由△=4(1-m)≥0,得m≤1.
①当m=1时,g′(x)=0有实根x=
 ,在x=
,在x= 左右两侧均有g′(x)>0,故函数g(x)无极值.
左右两侧均有g′(x)>0,故函数g(x)无极值.②当m<1时,g′(x)=0有两个实根,
x1=
 (2-
(2-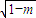 ),x2=
),x2= (2+
(2+ ),
),当x变化时,g′(x)、g(x)的变化情况如下表:

故在m∈(-∞,1)时,函数g(x)有极值;当x=
 (2-
(2- )时,g(x)有极大值;当x=
)时,g(x)有极大值;当x= (2+
(2+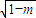 ) 时,g(x)有极小值.
) 时,g(x)有极小值.点评:本题考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目