题目内容
数列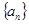
共有5项，其中
，
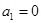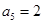，且
，
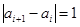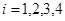，则满足条件的不同数列的个数为( )
| A．3 | B．4 | C．5 | D．6 |
B
解析试题分析：设
，
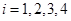，则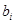
等于1或-1，
由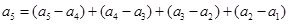
，
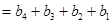知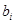
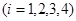共有3个1，1个-1.这种组合共有
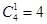个，选B.
考点：排列组合.
练习册系列答案
阅读快车系列答案
相关题目
将6名男生、4名女生分成两组，每组5人，参加两项不同的活动，每组3名男生和2名女生，则不同的分配方法有（ ）
| A．240种 | B．120种 | C．60种 | D．180种 |
从8名女生和4名男生中，抽取3名学生参加某档电视节目，如果按性别比例分层抽样，则不同的抽取方法数为( )
| A．224 | B．112 | C．56 | D．28 |
“渐升数” 是指每个数字比它左边的数字大的正整数(如1458) ,若把四位“渐升数”按从小到大的顺序排列.则第30个数为( )
| A．1278 | B．1346 | C．1359 | D．1579 |
二项式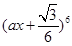
的展开式的第二项的系数为
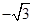，则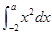
的值为（ ）
A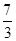． | B．3 | C．3或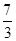 | D．3或 |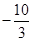
回文数是指从左到右读与从右到左读都一样的正整数，如22,121,3443,94249等．显然2位回文数有9个：11,22,33，…，99.3位回文数有90个：101,111,121，…，191,202，…，999.则2n＋1(n∈N*)位回文数的个数为（ ）
| A．9×10n-1个 | B．9×10n个 |
| C．9×10n+1个 | D．9×10n+2个 |
已知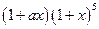
的展开式中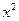
的系数为5,则a=( )
| A．－4 | B．－3 | C．－2 | D．－1 |
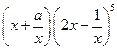的展开式中各项系数的和为2，则该展开式中常数项为（ ）
| A．-40 | B．-20 | C．20 | D．40 |
将甲、乙、丙等六人分配到高中三个年级，每个年级2人，要求甲必须在高一年级，乙和丙均不能在高三年级，则不同的安排种数为( )
| A．18 | B．15 | C．12 | D．9 |