题目内容
某地区为了解高二学生作业量和玩电脑游戏的情况,对该地区内所有高二学生采用随机抽样的方法,得到一个容量为200的样本.统计数据如下:

(1)已知该地区共有高二学生42500名,根据该样本估计总体,其中喜欢电脑游戏并认为作业不多的人有多少名?
(2)在A,B,C,D,E,F六名学生中,仅有A,B两名学生认为作业多.如果从这六名学生中随机抽取两名,求至少有一名学生认为作业多的概率.

(1)已知该地区共有高二学生42500名,根据该样本估计总体,其中喜欢电脑游戏并认为作业不多的人有多少名?
(2)在A,B,C,D,E,F六名学生中,仅有A,B两名学生认为作业多.如果从这六名学生中随机抽取两名,求至少有一名学生认为作业多的概率.
(1)7650名;(2)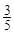
试题分析:(1)利用样本估计总体,可求得喜欢电脑游戏并认为作业不多的人数;(2)用列举法,并利用古典概型即可求得至少有一名学生认为作业多的概率
试题解析:(1)
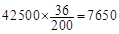 (名) 5分
(名) 5分(2)【方法一】从这六名学生中随机抽取两名的基本事件有:{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15个 7分
其中至少有一个学生认为作业多的事件有{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F}共9个 9分
∴
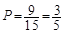
即至少有一名学生认为作业多的概率为
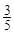 . 12分
. 12分【方法二】6名学生中随机抽取2名的选法有
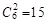 种, 7分
种, 7分其中至少有一名学生认为作业多的选法有
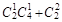 =9种, 9分
=9种, 9分∴
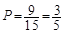
即至少有一名学生认为作业多的概率为
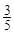 . 12分
. 12分【方法三】6名学生中随机抽取2名的选法有
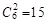 种, 7分
种, 7分其中没有人认为作业多的选法有
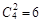 种 9分
种 9分∴
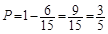
即至少有一名学生认为作业多的概率为
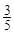 . 12分
. 12分
练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
 的值;
的值; 的车辆数;
的车辆数; 的概率.
的概率. .
.

 ,其中
,其中 )
) 道备选题中一次性随机抽取
道备选题中一次性随机抽取 道题,按照题目要求独立完成.规定:至少正确完成其中
道题,按照题目要求独立完成.规定:至少正确完成其中 道题的便可通过.已知
道题的便可通过.已知 道题能正确完成,
道题能正确完成, ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响. ,“第2次拿出的是白球”为事件
,“第2次拿出的是白球”为事件 ,则事件
,则事件



 ,
, ,点P的坐标为(
,点P的坐标为( ,
, ),
), ,
, ,则点P在直线
,则点P在直线 下方的概率为 .[
下方的概率为 .[ 


