题目内容
已知定义在[1,8]上的函数f(x)=
,该函数的值域是
|
[0,4]
[0,4]
.分析:对于分段函数可先分段考虑:当1≤x≤2时,利用绝对值函数画出其图象,当2<x≤4时,1<
≤2,此时f(x)=
f(
)=
(4-8|
-
|),当4<x≤8时,1<
≤2,此时f(x)=
f(
)=
×
×f(
)=
(4-8|
-
|),分别在坐标系中画出f(x)在(4,8]上的图象,最后观察图象得出该函数的值域.
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 3 |
| 2 |
| x |
| 4 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 4 |
| 1 |
| 4 |
| x |
| 4 |
| 3 |
| 2 |
解答: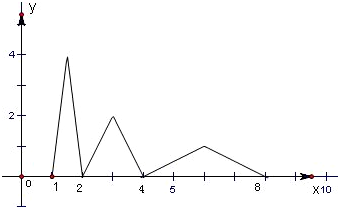 解:当1≤x≤2时,
解:当1≤x≤2时,
f(x)=4-8|x-
|=
,
在坐标系中画出f(x)在[1,2]上的图象,如图中所示.
当2<x≤4时,1<
≤2,此时
f(x)=
f(
)=
(4-8|
-
|),同样在坐标系中画出f(x)在(2,4]上的图象,如图中所示.
当4<x≤8时,1<
≤2,此时
f(x)=
f(
)=
×
×f(
)=
(4-8|
-
|),同样在坐标系中画出f(x)在(4,8]上的图象,如图中所示.
观察图象可知,该函数的值域是[0,4].
故答案为:[0,4].
 解:当1≤x≤2时,
解:当1≤x≤2时,f(x)=4-8|x-
| 3 |
| 2 |
|
在坐标系中画出f(x)在[1,2]上的图象,如图中所示.
当2<x≤4时,1<
| x |
| 2 |
f(x)=
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 3 |
| 2 |
当4<x≤8时,1<
| x |
| 4 |
f(x)=
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 4 |
| 1 |
| 4 |
| x |
| 4 |
| 3 |
| 2 |
观察图象可知,该函数的值域是[0,4].
故答案为:[0,4].
点评:本小题主要考查分段函数的应用、函数的值域等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知定义在[1,8]上的函数f(x)=
.则下列结论中,错误的是( )
|
| A、f(3)=2 |
| B、函数f(x)的值域为[0,4] |
| C、对任意的x∈[1,8],不等式xf(x)≤6恒成立 |
| D、将函数f(x)的极值由大到小排列得到数列{an},n∈N*,则{an}为等比数列 |
已知定义在[1,8]上的函数 f(x)=
则下列结论中,错误的是( )
|
| A、f(6)=1 |
| B、函数f(x)的值域为[0,4] |
| C、将函数f(x)的极值由大到小排列得到数列{an},n∈N*,则{an}为等比数列 |
| D、对任意的x∈[1,8],不等式xf(x)≤6恒成立 |
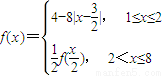 则下列结论中,错误的是( )
则下列结论中,错误的是( )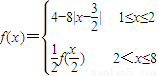 .则下列结论中,错误的是( )
.则下列结论中,错误的是( )