题目内容
已知曲线C是动点M到两个定点O(0,0)、A(3,0)距离之比为
的点的轨迹.
(1)求曲线C的方程;
(2)求过点N(1,3)与曲线C相切的直线方程.
| 1 | 2 |
(1)求曲线C的方程;
(2)求过点N(1,3)与曲线C相切的直线方程.
分析:(1)设点M(x,y),利用两点之间的距离公式,将|OM|、|AM|表示成关于x、y的式子,利用它们的距离之比为
建立等式,化简整理即可得到曲线C的方程;
(2)由(1)得曲线C是以(-1,0)为圆心,半径r=2的圆.然后按直线的斜率是否存在进行分类讨论,结合点到直线的距离公式加以计算,即可得到两条切线的方程.
| 1 |
| 2 |
(2)由(1)得曲线C是以(-1,0)为圆心,半径r=2的圆.然后按直线的斜率是否存在进行分类讨论,结合点到直线的距离公式加以计算,即可得到两条切线的方程.
解答:解:(1)设点M(x,y),则
|OM|=
,|AM|=
∵
=
,∴|AM|=2|OM|即
=2
…4分
两边平方整理,得:x2+y2+2x-3=0,即为所求曲线C的方程.…6分
(2)由(1)得x2+y2+2x-3=0,整理得(x+1)2+y2=4
∴曲线C是以(-1,0)为圆心,半径r=2的圆.
i)当过点N(1,3)的直线的斜率不存在时,直线方程为x=1,显然与圆相切;…8分
ii) 当过点N(1,3)的直线的斜率存在时,设方程为y-3=k(x-1)
即kx-y+3-k=0 …9分
∵直线与圆相切.得圆心到该直线的距离等于半径,
∴
=2,解之得k=
,…11分
可得直线方程为5x-12y+31=0 …12分
所以过点N(1,3)与曲线C相切的直线方程为x=1或5x-12y+31=0.…13分
|OM|=
| x2+y2 |
| (x-3)2+y2 |
∵
| |OM| |
| |AM| |
| 1 |
| 2 |
| (x-3)2+y2 |
| x2+y2 |
两边平方整理,得:x2+y2+2x-3=0,即为所求曲线C的方程.…6分
(2)由(1)得x2+y2+2x-3=0,整理得(x+1)2+y2=4
∴曲线C是以(-1,0)为圆心,半径r=2的圆.
i)当过点N(1,3)的直线的斜率不存在时,直线方程为x=1,显然与圆相切;…8分
ii) 当过点N(1,3)的直线的斜率存在时,设方程为y-3=k(x-1)
即kx-y+3-k=0 …9分
∵直线与圆相切.得圆心到该直线的距离等于半径,
∴
| |-k+0+3-k| | ||
|
| 5 |
| 12 |
可得直线方程为5x-12y+31=0 …12分
所以过点N(1,3)与曲线C相切的直线方程为x=1或5x-12y+31=0.…13分
点评:本题给出满足条件的动点,求轨迹方程并求与曲线相切的直线方程,着重考查了直线与圆的位置关系和轨迹方程的求法等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和到直线y=
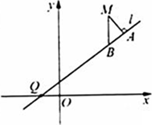
和到直线y= 距离相等的点的轨迹,l是过点Q(-1,0)的直线,M是C上(不在l上)的动点;A、B在l上,MA⊥l,MB⊥x轴(如图),
距离相等的点的轨迹,l是过点Q(-1,0)的直线,M是C上(不在l上)的动点;A、B在l上,MA⊥l,MB⊥x轴(如图), 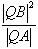 为常数。
为常数。
 的点的轨迹.
的点的轨迹.