题目内容
(2012•浙江模拟)已知集合A={(x,y)|
},集合B={(x,y)|xcosα+ysinα-1=0,α∈[0,2π)},若A∩B≠∅,则α的取值范围是
|
[0,
]∪[
,2π)
| π |
| 2 |
| 7π |
| 4 |
[0,
]∪[
,2π)
.| π |
| 2 |
| 7π |
| 4 |
分析:画出约束条件表示的可行域,集合B表示的区域,通过A∩B≠∅,求出α的取值范围.
解答: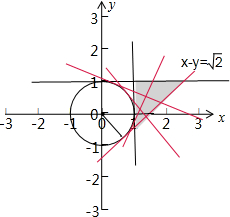 解:由题意集合A={(x,y)|
解:由题意集合A={(x,y)|
}表示的可行域如图三角形,
集合B={(x,y)|xcosα+ysinα-1=0,α∈[0,2π)},表示的区域是单位圆的切线,若A∩B≠∅,即图中红色直线与集合A表示的可行域有交点,所以α∈[0,
]∪[
,2π),
故答案为:[0,
]∪[
,2π).
 解:由题意集合A={(x,y)|
解:由题意集合A={(x,y)|
|
集合B={(x,y)|xcosα+ysinα-1=0,α∈[0,2π)},表示的区域是单位圆的切线,若A∩B≠∅,即图中红色直线与集合A表示的可行域有交点,所以α∈[0,
| π |
| 2 |
| 7π |
| 4 |
故答案为:[0,
| π |
| 2 |
| 7π |
| 4 |
点评:本题考查线性规划的应用,集合的基本关系,判断集合B的图形是解题的关键,考查转化思想,计算能力.

练习册系列答案
相关题目
 (2012•浙江模拟)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )
(2012•浙江模拟)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )