题目内容
某工厂生产某种水杯，每个水杯的原材料费、加工费分别为30元、m元（m为常数，且2≤m≤3），设每个水杯的出厂价为x元（35≤x≤41），根据市场调查，水杯的日销售量与ex（e为自然对数的底数）成反比例，已知每个水杯的出厂价为40元时，日销售量为10个．
（Ⅰ）求该工厂的日利润y（元）与每个水杯的出厂价x（元）的函数关系式；
（Ⅱ）当每个水杯的出厂价为多少元时，该工厂的日利润最大，并求日利润的最大值．
解：（Ⅰ）设日销量为s，则s=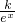
∵x=40，s=10，∴10=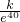
，∴k=10e40，∴s=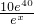
∴y=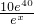（x-30-m）（35≤x≤40）；
（Ⅱ）y′=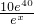（31+m-x），令y′=0，可得x=31+m
∴当2≤m≤3时，33≤31+m≤34，y′＜0，∴当35≤x≤41时，函数为减函数．
∴当x=35时，y取最大值，最大值为10（5-t）e5．
分析：（Ⅰ）由条件“日销售量与ex（e为自然对数的底数）成反比例”可设日销量，根据日利润y=每件的利润×件数，建立函数关系式，注意实际问题自变量的范围．
（Ⅱ）先对函数进行求导，求出极值点，利用2≤m≤3，可得函数在35≤x≤41范围内的单调性，从而求出函数的最值．
点评：本题考查函数模型的构建，考查导数知识的运用，解题的关键在于建立数学模型和目标函数，属于中档题．
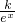
∵x=40，s=10，∴10=
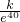，∴k=10e40，∴s=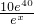∴y=
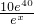（x-30-m）（35≤x≤40）；（Ⅱ）y′=
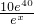（31+m-x），令y′=0，可得x=31+m∴当2≤m≤3时，33≤31+m≤34，y′＜0，∴当35≤x≤41时，函数为减函数．
∴当x=35时，y取最大值，最大值为10（5-t）e5．
分析：（Ⅰ）由条件“日销售量与ex（e为自然对数的底数）成反比例”可设日销量，根据日利润y=每件的利润×件数，建立函数关系式，注意实际问题自变量的范围．
（Ⅱ）先对函数进行求导，求出极值点，利用2≤m≤3，可得函数在35≤x≤41范围内的单调性，从而求出函数的最值．
点评：本题考查函数模型的构建，考查导数知识的运用，解题的关键在于建立数学模型和目标函数，属于中档题．
练习册系列答案
考前必练系列答案
相关题目