题目内容
(12分)数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() (
(![]() ).
).
(Ⅰ)证明数列![]() 是等比数列,求出数列
是等比数列,求出数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)数列![]() 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
(Ⅰ)因为![]() ,所以
,所以![]() ,
,
则![]() ,所以
,所以![]() ,
,![]() ,
,
数列![]() 是等比数列,…………3分
是等比数列,…………3分
![]() ,
,![]() ,
,
所以![]() .………………4分
.………………4分
(Ⅱ)![]() ,…………5分
,…………5分
![]() ,
,
令![]() ,①
,①
![]() ,②
,②
①-②得,![]() ,
,
![]() ,…………7分
,…………7分
所以![]() .…………8分
.…………8分
(Ⅲ)设存在![]() ,且
,且![]() ,使得
,使得![]() 成等差数列,则
成等差数列,则![]() ,
,
即![]() ,…………10分
,…………10分
即![]() ,
,![]() ,
,![]() 为偶数,而
为偶数,而![]() 为奇数,
为奇数,
所以![]() 不成立,故不存在满足条件的三项.…… 12分
不成立,故不存在满足条件的三项.…… 12分

练习册系列答案
相关题目
 为等差数列,
为等差数列, ,
, ,数列
,数列 的前
的前 项和为
项和为 ,且有
,且有
 ,
, 的前
的前 ,求
,求 的大小,并说明理由.
的大小,并说明理由. 的前
的前 项和为
项和为 ,且对
,且对 都有
都有 ,则:
,则: ;
; 上述结果,归纳猜想数列
上述结果,归纳猜想数列 公式,并用数学归纳法加以证明.
公式,并用数学归纳法加以证明. .
. 的前
的前 项和为
项和为 ,且
,且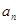 是
是 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,证明:
,证明: .
.