题目内容
建筑一个容积为8000米3,深6米的长方体蓄水池(无盖),池壁造价为a元/米2,池底造价为2a元/米2,把总造价y元表示为一底的边长x米的函数________.
y=6ax+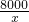 a+
a+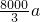 .
.
分析:水池长为x,宽为m,高为6,则6xm=8000,xm= ,m=
,m=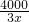 ,再由题设条件分别求出池底造价,池壁造价,由此可可求出总造价.
,再由题设条件分别求出池底造价,池壁造价,由此可可求出总造价.
解答:设水池长为x,宽为m,高为6,
根据题意有6xm=8000,则xm= ,m=
,m=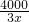 ,
,
所以池底的面积为 平方米,池底造价为:
平方米,池底造价为: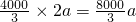 元,
元,
池壁面积为:6(x+m),所以池壁造价为:6(x+m)a=6ax+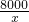 a元,
a元,
∴总造价y=6ax+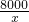 a+
a+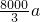 .
.
故答案为y=6ax+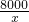 a+
a+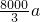 .
.
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答.
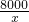 a+
a+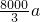 .
.分析:水池长为x,宽为m,高为6,则6xm=8000,xm=
 ,m=
,m=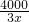 ,再由题设条件分别求出池底造价,池壁造价,由此可可求出总造价.
,再由题设条件分别求出池底造价,池壁造价,由此可可求出总造价.解答:设水池长为x,宽为m,高为6,
根据题意有6xm=8000,则xm=
 ,m=
,m=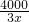 ,
,所以池底的面积为
 平方米,池底造价为:
平方米,池底造价为: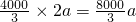 元,
元,池壁面积为:6(x+m),所以池壁造价为:6(x+m)a=6ax+
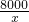 a元,
a元,∴总造价y=6ax+
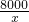 a+
a+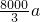 .
.故答案为y=6ax+
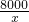 a+
a+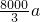 .
.点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目