题目内容

（2013•东城区一模）不等式组
x-2≤0
y≤0
x+y≥0
表示的平面区域为D，则区域D的面积为
2
2
，z=x+y的最大值为
2
2
．
分析：先画出可行域，再利用三角形面积公式求第一问；第二问需由z=x+y，再变形为y=-x+z，则过点B时z最大．
解答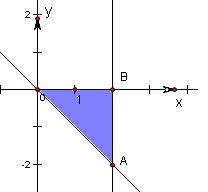：解：不等式组所表示的平面区域如图所示
解得A（2，-2）、B（2，0）、C（0，0），
所以S△ABC=
1
2
×2×2=2；
由z=x+y，则y=-x+z，
所以直线经过点B时x+y取得最大值，最大值为2+0=2．
故答案为：2，2．
点评：本类题是解决线性规划问题，本类题常用的步骤有两种：一是：由约束条件画出可行域，求出可行域各个角点的坐标，将坐标逐一代入目标函数，验证，求出最优解．二是：画出可行域，标明函数几何意义，确定最优解．
练习册系列答案
相关题目
（2013•东城区一模）设A是由n个有序实数构成的一个数组，记作：A=（a1，a2，…，ai，…，an）．其中ai（i=1，2，…，n）称为数组A的“元”，S称为A的下标．如果数组S中的每个“元”都是来自 数组A中不同下标的“元”，则称A=（a1，a2，…，an）为B=（b1，b2，…bn）的子数组．定义两个数组A=（a1，a2，…，an），B=（b1，b2，…，bn）的关系数为C（A，B）=a1b1+a2b2+…+anbn．
（Ⅰ）若A=(-
1
2
，
1
2
)，B=（-1，1，2，3），设S是B的含有两个“元”的子数组，求C（A，S）的最大值；
（Ⅱ）若A=(
3
3
，
3
3
，
3
3
)，B=（0，a，b，c），且a2+b2+c2=1，S为B的含有三个“元”的子数组，求C（A，S）的最大值．
（2013•东城区一模）某游戏规则如下：随机地往半径为1的圆内投掷飞标，若飞标到圆心的距离大于
1
2
，则成绩为及格；若飞标到圆心的距离小于
1
4
，则成绩为优秀；若飞标到圆心的距离大于
1
4
且小于
1
2
，则成绩为良好，那么在所有投掷到圆内的飞标中得到成绩为良好的概率为（　　）
（2013•东城区一模）函数f(x)=sin(x-
π
3
)的图象为C，有如下结论：
①图象C关于直线x=
5π
6
对称；
②图象C关于点(
4π
3
，0)对称；
③函数f（x）在区间[
π
3
，
5π
6
]内是增函数，
其中正确的结论序号是
①②③
①②③
．（写出所有正确结论的序号）
（2013•东城区一模）已知全集U={1，2，3，4}，集合A={1，2}，那么集合?UA为（　　）
（2013•东城区一模）数列{an}的各项排成如图所示的三角形形状，其中每一行比上一行增加两项，若an=an（a≠0），则位于第10行的第8列的项等于
a89
a89
，a2013在图中位于
第45行的第77列
第45行的第77列
．（填第几行的第几列）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网