题目内容
设双曲线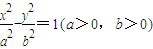 的离心率为
的离心率为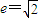 ,右焦点为f(c,0),方程ax2-bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )
,右焦点为f(c,0),方程ax2-bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )A.在圆x2+y2=8外
B.在圆x2+y2=8上
C.在圆x2+y2=8内
D.不在圆x2+y2=8内
【答案】分析:由已知圆的方程找出圆心坐标与圆的半径r,然后根据双曲线的离心率公式找出c与a的关系,根据双曲线的平方关系,把c与a的关系代入即可得到a等于b,然后根据韦达定理表示出两根之和和两根之积,利用两点间的距离公式表示出点P与圆心的距离,把a,b及c的关系代入即可求出值,与圆的半径比较大小即可判断出点与圆的位置关系.
解答:解:由圆的方程x2+y2=8得到圆心O坐标为(0,0),圆的半径r=2 ,
,
又双曲线的离心率为e= =
= ,即c=
,即c= a,
a,
则c2=2a2=a2+b2,即a2=b2,又a>0,b>0,得到a=b,
因为方程ax2-bx-c=0的两个实根分别为x1和x2,所以x1+x2= ,x1x2=-
,x1x2=- ,
,
则|OP|= =
= =
= =
= <r=2
<r=2 ,
,
所以点P在圆x2+y2=8内.
故选C
点评:此题考查学生掌握点与圆的位置关系的判别方法,灵活运用韦达定理及两点间的距离公式化简求值,是一道中档题.
解答:解:由圆的方程x2+y2=8得到圆心O坐标为(0,0),圆的半径r=2
 ,
,又双曲线的离心率为e=
 =
= ,即c=
,即c= a,
a,则c2=2a2=a2+b2,即a2=b2,又a>0,b>0,得到a=b,
因为方程ax2-bx-c=0的两个实根分别为x1和x2,所以x1+x2=
 ,x1x2=-
,x1x2=- ,
,则|OP|=
 =
= =
= =
= <r=2
<r=2 ,
,所以点P在圆x2+y2=8内.
故选C
点评:此题考查学生掌握点与圆的位置关系的判别方法,灵活运用韦达定理及两点间的距离公式化简求值,是一道中档题.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,且它的一条准线与抛物线
,且它的一条准线与抛物线 的准线重合,则此双曲线的方程为
的准线重合,则此双曲线的方程为 B.
B.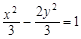 C.
C. D.
D.
 的离心率为
的离心率为 ,且它的一条准线与抛物线
,且它的一条准线与抛物线 的准线重合,则此双曲线的方程为( )
的准线重合,则此双曲线的方程为( ) B.
B.
 D.
D.