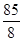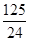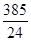题目内容
在平面直角坐标系中,记抛物线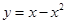 与x轴所围成的平面区域为
与x轴所围成的平面区域为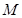 ,该抛物线与直线y=
,该抛物线与直线y=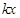 (k>0)所围成的平面区域为
(k>0)所围成的平面区域为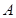 ,向区域
,向区域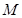 内随机抛掷一点
内随机抛掷一点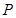 ,若点
,若点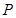 落在区域
落在区域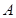 内的概率为
内的概率为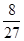 ,则k的值为( )
,则k的值为( )
A. | B.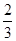 | C.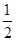 | D.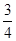 |
A
解析试题分析:∵ ,
, ,
,
∴ ,∴
,∴ ,故选A.
,故选A.
考点:1.积分的运算;2.几何概型.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知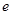 为自然对数的底数,设函数
为自然对数的底数,设函数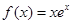 ,则( )
,则( )
A. 是 是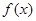 的极小值点 的极小值点 | B.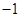 是 是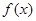 的极小值点 的极小值点 |
C. 是 是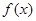 的极大值点 的极大值点 | D.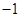 是 是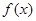 的极大值点 的极大值点 |
曲线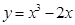 在
在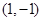 处的切线方程为( )
处的切线方程为( )
A.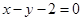 | B.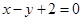 | C.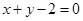 | D.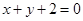 |
已知函数f(x)=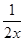 -cosx,若
-cosx,若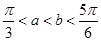 ,则( )
,则( )
| A.f(a)>f(b) | B.f(a)<f(b) | C.f(a)=f(b) | D.f(a)f(b)>0 |
已知函数f(x)=-x3+ax2-4在x=2处取得极值,若m,n∈[-1,1],则f(m)+f'(n)的最小值为( )
| A.-13 | B.-15 | C.10 | D.15 |
某汽车启动阶段的路程函数为s(t)=2t3-5t2+2,则t=2秒时,汽车的加速度是( ).
| A.14 | B.4 |
| C.10 | D.6 |
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,
则f(x)>2x+4的解集为 ( ).
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
已知函数y=f(x)的图象关于y轴对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,a=(20.2)·f(20.2),b=(logπ3)·f(logπ3),c=(log39)·f(log39),则a,b,c的大小关系是( )
| A.b>a>c | B.c>a>b |
| C.c>b>a | D.a>c>b |
 的方向向量为
的方向向量为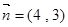 且过抛物线
且过抛物线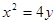 的焦点,则直线
的焦点,则直线