题目内容
老师给出一个函数,请三位同学各说出了这个函数的一条性质:
①此函数为偶函数;②定义域为{x∈R|x≠0};③在(0,+∞)上为增函数.
老师评价说其中有一个同学的结论错误,另两位同学的结论正确.请你写出一个这样的函数
①此函数为偶函数;②定义域为{x∈R|x≠0};③在(0,+∞)上为增函数.
老师评价说其中有一个同学的结论错误,另两位同学的结论正确.请你写出一个这样的函数
f(x)=x2
f(x)=x2
.分析:由题意可得,要求的函数满足性质①②③中的两个,这样的函数有多个,再由函数f(x)=x2 满足①③,不满足②,从而得到答案.
解答:解:由题意可得:要求的函数满足下列三条性质中的两条:①此函数为偶函数;②定义域为{x∈R|x≠0};③在(0,+∞)上为增函数,
故这样的函数有多个,其中,函数f(x)=x2 满足①③,不满足②,符合题意,
故答案为f(x)=x2,(答案不唯一).
故这样的函数有多个,其中,函数f(x)=x2 满足①③,不满足②,符合题意,
故答案为f(x)=x2,(答案不唯一).
点评:本题主要考查函数的奇偶性和单调性的应用,属于基础题.

练习册系列答案
相关题目
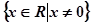 ;
;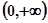 上为增函数.
上为增函数.