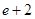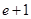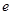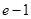题目内容
已知函数f(x)=2x+
+alnx,a∈R.
(1)若函数f(x)在[1,+∞)上单调递增,求实数a的取值范围.
(2)记函数g(x)=x2[f′(x)+2x-2],若g(x)的最小值是-6,求函数f(x)的解析式.
| 2 |
| x |
(1)若函数f(x)在[1,+∞)上单调递增,求实数a的取值范围.
(2)记函数g(x)=x2[f′(x)+2x-2],若g(x)的最小值是-6,求函数f(x)的解析式.
(本小题满分14分)
(1)f′(x)=2-
+
≥0,
∴a≥
-2x在[1,+∞)上恒成立…(2分)
令h(x)=
-2x,x∈[1,+∞)
∵h′(x)=-
-2<0恒成立,
∴h(x)在[1,+∞)单调递减…(4分)
h(x)max=h(1)=0…(6分)
∴a≥0,
故实数a的取值范围为[0,+∞).…(7分)
(2)g(x)=2x3+ax-2,x>0
∵g′(x)=6x2+a…(9分)
当a≥0时,g′(x)≥0恒成立,
∴g(x)在(0,+∞)单调递增,无最小值,不合题意,
∴a<0.…(11分)
令g′(x)=0,则x=
(舍负)
∵0<x<
时,g′(x)<0;x>
时,g′(x)>0,
∴g(x)在(0,
)上单调递减,在(
+∞)上单调递增,
则x=
是函数的极小值点.g(x)min=g(x)极小=g(
)=-6.…(13分)
解得a=-6,
故f(x)=2x+
-6lnx.…(14分)
(1)f′(x)=2-
| 2 |
| x2 |
| a |
| x |
∴a≥
| 2 |
| x |
令h(x)=
| 2 |
| x |
∵h′(x)=-
| 2 |
| x2 |
∴h(x)在[1,+∞)单调递减…(4分)
h(x)max=h(1)=0…(6分)
∴a≥0,
故实数a的取值范围为[0,+∞).…(7分)
(2)g(x)=2x3+ax-2,x>0
∵g′(x)=6x2+a…(9分)
当a≥0时,g′(x)≥0恒成立,
∴g(x)在(0,+∞)单调递增,无最小值,不合题意,
∴a<0.…(11分)
令g′(x)=0,则x=
|
∵0<x<
|
|
∴g(x)在(0,
|
|
则x=
|
|
解得a=-6,
故f(x)=2x+
| 2 |
| x |

练习册系列答案
相关题目

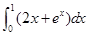 的值为( )
的值为( )