题目内容
选修4—1:几何证明选讲
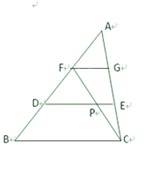
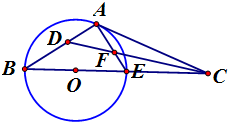
如图:在Rt∠ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作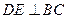 ,垂足为E,连接AE交⊙O于点F,求证:
,垂足为E,连接AE交⊙O于点F,求证: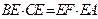 。
。

如图:在Rt∠ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作
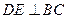 ,垂足为E,连接AE交⊙O于点F,求证:
,垂足为E,连接AE交⊙O于点F,求证: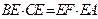 。
。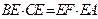
证明:(方法一)因为
所以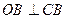
所以CB为⊙O的切线 2分
所以EB2=EF·FA 5分
连结OD,因为AB=BC
所以
所以
在四边形BODE中,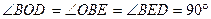
所以BODE为矩形 7分
所以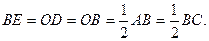
即
所以 10分
10分
(方法二)因为
所以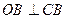 ,所以CB为⊙O的切线 2分
,所以CB为⊙O的切线 2分
所以EB2=EF·FA 5分
连结BD,因为AB是⊙O的直径,
所以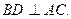
又因为AB=BC,
所以AD=BD=DC。 7分
因为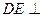 BC,所以BE=CE。
BC,所以BE=CE。
所以 10分
10分

所以
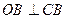
所以CB为⊙O的切线 2分
所以EB2=EF·FA 5分
连结OD,因为AB=BC
所以

所以

在四边形BODE中,
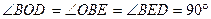
所以BODE为矩形 7分
所以
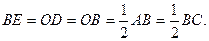
即

所以
 10分
10分(方法二)因为

所以
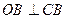 ,所以CB为⊙O的切线 2分
,所以CB为⊙O的切线 2分所以EB2=EF·FA 5分
连结BD,因为AB是⊙O的直径,
所以
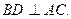
又因为AB=BC,
所以AD=BD=DC。 7分
因为
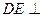 BC,所以BE=CE。
BC,所以BE=CE。所以
 10分
10分
练习册系列答案
相关题目

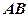
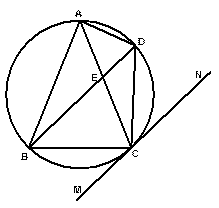
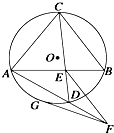
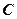 是内接于⊙O,
是内接于⊙O,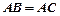 ,直线
,直线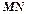 切⊙O于点
切⊙O于点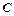 ,弦
,弦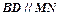 ,
,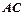 与
与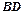 相交于点
相交于点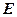 .
.
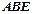 ≌Δ
≌Δ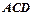 ;
;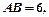
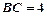 ,求
,求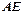 .
.
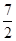
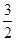
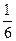 ,且满足
,且满足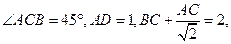 则
则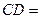 .
.