题目内容
函数y=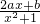 的最大值为4,最小值为-1,求常数a、b的值.
的最大值为4,最小值为-1,求常数a、b的值.
解:由y=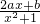 去分母整理得
去分母整理得
yx2-2ax+y-b=0.①
对于①,有实根的条件是△≥0,
即(-2a)2-4y(y-b)≥0.
∴y2-by-a2≤0.又-1≤y≤4,
∴y2-by-a2=0的两根为-1和4.
∴ 解得
解得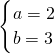 或
或
分析:由y=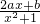 去分母整理得yx2-2ax+y-b=0,将y看作是系数,此方程一定有解,故判别式△≥0,由此得到关于y的不等式,数y=
去分母整理得yx2-2ax+y-b=0,将y看作是系数,此方程一定有解,故判别式△≥0,由此得到关于y的不等式,数y=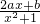 的最大值为4,最小值为-1,故y2-by-a2=0的两根为-1和4.再用根系关系建立起常数a,b的方程,求值.
的最大值为4,最小值为-1,故y2-by-a2=0的两根为-1和4.再用根系关系建立起常数a,b的方程,求值.
点评:本题考点是函数的值域,考查了判别式法求值域的变形运用,得到了关于函数值y的不等式,再由根系关系建立关于所求参数的方程求参数,此方法是解决分式型二次函数值域求法的便捷方法,注意研究其特征及做题过程.
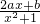 去分母整理得
去分母整理得yx2-2ax+y-b=0.①
对于①,有实根的条件是△≥0,
即(-2a)2-4y(y-b)≥0.
∴y2-by-a2≤0.又-1≤y≤4,
∴y2-by-a2=0的两根为-1和4.
∴
 解得
解得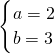 或
或
分析:由y=
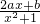 去分母整理得yx2-2ax+y-b=0,将y看作是系数,此方程一定有解,故判别式△≥0,由此得到关于y的不等式,数y=
去分母整理得yx2-2ax+y-b=0,将y看作是系数,此方程一定有解,故判别式△≥0,由此得到关于y的不等式,数y=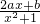 的最大值为4,最小值为-1,故y2-by-a2=0的两根为-1和4.再用根系关系建立起常数a,b的方程,求值.
的最大值为4,最小值为-1,故y2-by-a2=0的两根为-1和4.再用根系关系建立起常数a,b的方程,求值.点评:本题考点是函数的值域,考查了判别式法求值域的变形运用,得到了关于函数值y的不等式,再由根系关系建立关于所求参数的方程求参数,此方法是解决分式型二次函数值域求法的便捷方法,注意研究其特征及做题过程.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ,若函数z=x+y的最大值为4,则实数a的值为
,若函数z=x+y的最大值为4,则实数a的值为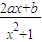 的最大值为4,最小值为-1,求常数a、b的值.
的最大值为4,最小值为-1,求常数a、b的值.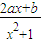 的最大值为4,最小值为-1,求常数a、b的值.
的最大值为4,最小值为-1,求常数a、b的值.