Question

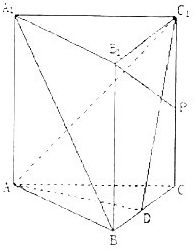如图，在正三棱柱ABC-A₁B₁C₁中，AB=AA₁，D是BC的中点，P是CC₁的中点．求证：
（1）A₁B∥平面AC₁D；
（2）B₁P⊥平面AC₁D．

Answer 1

分析：（1）连接A₁C交AC₁于点O，连接OD，根据OD是△A₁CB的中位线可得OD∥A₁B，又A₁B?平面AC₁D，OD?平面AC₁D，从而证得
A₁B∥平面AC₁D．
（2）由（1）知，∴△CC₁D≌△C₁B₁P，故∠CDC₁=∠C₁PB₁，B₁P⊥C₁D．再由AD⊥平面BCC₁B₁，可得AD⊥B₁P，从而证得
B₁P⊥平面AC₁D．

解答：证明：（1）连接A₁C交AC₁于点O，连接OD，在正三棱柱ABC-A₁B₁C₁中，AB=AA₁，∴侧面AA₁C₁C是正方形，
∴点O是AC₁的中点，又点D是BC的中点，故OD是△A₁CB的中位线．
∴OD∥A₁B，又A₁B?平面AC₁D，OD?平面AC₁D，∴A₁B∥平面AC₁D． …（7分）
（2）由（1）知，侧面BCC₁B₁是正方形，又D、P分别为BC、CC₁的中点，∴△CC₁D≌△C₁B₁P，
∴∠CDC₁=∠C₁PB₁，∴B₁P⊥C₁D，…（9分）
在正三棱柱ABC-A₁B₁C₁中，D是BC的中点，∴AD⊥BC，又侧面BCC₁B₁⊥底面ABC，且侧面BCC₁B₁∩底面ABC=BC，
AD?底面ABC，∴AD⊥平面BCC₁B₁，…（12分）
又B₁P?平面BCC₁B₁，∴AD⊥B₁P，又AD∩C₁D=D，∴B₁P⊥平面AC₁D．…（14分）

点评：本题考查证明线面平行、线面垂直的方法，直线和平面平行的判定定理以及直线和平面垂直的判定定理的应用求，属于中档题．