题目内容
(本题14分)
已知函数 ,实数a,b为常数),
,实数a,b为常数),
(1)若a=1, 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程 在(0,1]上解的个数。
在(0,1]上解的个数。
【答案】
(1)b≥2
(2)解的个数为0个
【解析】(1)
①当
由条件,得 ≥0恒成立,即b≥x恒成立。[来源:]
≥0恒成立,即b≥x恒成立。[来源:]
∴b≥2
②当
由条件,得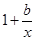 ≥0恒成立,即b≥-x恒成立
≥0恒成立,即b≥-x恒成立
∴b≥-2
∵f (x)的图象在(0,+∞)不间断,
综合①,②得b的取值范围是b≥2。
(2)令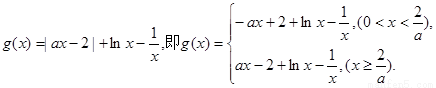
当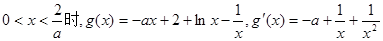 ,[来源:学.科.网]
,[来源:学.科.网]
∵
即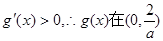 上是单调增函数。
上是单调增函数。
当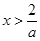 时,
时,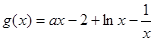 ,
,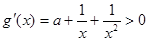
∴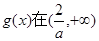 上是单调增函数。
上是单调增函数。
∵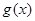 的图象在
的图象在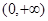 上不间断,∴
上不间断,∴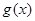 在
在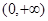 上是单调增函数。
上是单调增函数。
∵
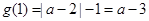
①当a≥3时,∵g (1) ≥0,∴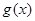 =0在(0,1]上有惟一解。
=0在(0,1]上有惟一解。
即方程 解的个数为1个。
解的个数为1个。
②当2≤a<3时,∵g (1) <0,∴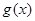 =0在(0,1]上无解。
=0在(0,1]上无解。
即方程 解的个数为0个。
解的个数为0个。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的内角,
的内角,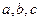 分别是其对边长,向量
分别是其对边长,向量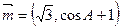 ,
,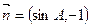 ,
,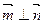
 求
求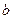 的长.
的长. 动点
动点 到定直线
到定直线 的距离等于
的距离等于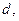 并且满足
并且满足 其中O是坐标原点,
其中O是坐标原点, 是参数.
是参数. 时,求
时,求 的最大值和最小值;
的最大值和最小值; 满足
满足 求实数
求实数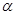 终边上一点
终边上一点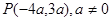 ,求
,求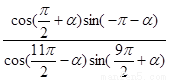 的值
的值 的左右两个焦点,O为坐标原点,点P
的左右两个焦点,O为坐标原点,点P 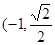 )在椭圆上,线段PB与y轴的交点M为线段PB的中点。
)在椭圆上,线段PB与y轴的交点M为线段PB的中点。 是椭圆上异于长轴端点的任一点,对于△ABC,求
是椭圆上异于长轴端点的任一点,对于△ABC,求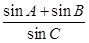 的值。
的值。