题目内容
设椭圆 的左右焦点分别为F1、F2A是椭圆C上的一点,且
的左右焦点分别为F1、F2A是椭圆C上的一点,且 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为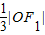 .
.(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过点Q的直线l交x轴于点F(-1,0),交y轴于点M,若|MQ|=2|QF|,求直线l的斜率.
【答案】分析:(1)题设知F1和F2的坐标,根据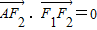 ,推断有
,推断有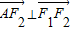 ,设点A的坐标为根据原点O到直线AF1的距离求得a,进而求得b.答案可得.
,设点A的坐标为根据原点O到直线AF1的距离求得a,进而求得b.答案可得.
(2)设直线斜率为k,则直线l的方程为y=k(x+1),设Q(x1,y1),由于Q,F,三点共线,且|MQ|=|2QF|.进而可得(x1,y1-k)=±2(x1+1,y),求得x1和y1,代入椭圆方程即可求得k,进而得到直线斜率.
解答:解:(1)由题设知F1(-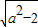 ,0),F2(
,0),F2(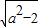 ,0),其中a>
,0),其中a>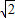
由于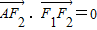 ,则有
,则有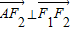 ,所以点A的坐标为(
,所以点A的坐标为(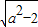 ±
±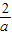
故AF1所在直线方程为y=±(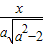 ),所以坐标原点O到直线AF1的距离为
),所以坐标原点O到直线AF1的距离为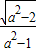 ,
,
又|OF1|=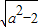 ,所以
,所以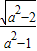 =|=
=|=
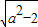 ,解得:a=2.
,解得:a=2.
∴所求椭圆的方程为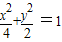 .
.
(2)由题意可知直线l的斜率存在,设直线斜率为k,则直线l的方程为y=k(x+1),故M(0,k).
设Q(x1,y1),由于Q,F,三点共线,且|MQ|=|2QF|.
根据题意得(x1,y1-k)=±2(x1+1,y1),解得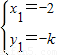 或
或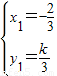
又Q在椭圆C上,故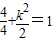 或
或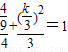 ,
,
解得k=0,k=±4,综上,直线的斜率为0或±4
点评:本题主要考查了椭圆的标准方程和直线与椭圆的关系.常需要直线方程和椭圆方程联立,根据韦达定理求得问题.
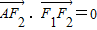 ,推断有
,推断有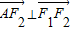 ,设点A的坐标为根据原点O到直线AF1的距离求得a,进而求得b.答案可得.
,设点A的坐标为根据原点O到直线AF1的距离求得a,进而求得b.答案可得.(2)设直线斜率为k,则直线l的方程为y=k(x+1),设Q(x1,y1),由于Q,F,三点共线,且|MQ|=|2QF|.进而可得(x1,y1-k)=±2(x1+1,y),求得x1和y1,代入椭圆方程即可求得k,进而得到直线斜率.
解答:解:(1)由题设知F1(-
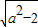 ,0),F2(
,0),F2(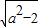 ,0),其中a>
,0),其中a>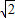
由于
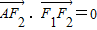 ,则有
,则有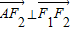 ,所以点A的坐标为(
,所以点A的坐标为(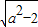 ±
±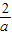
故AF1所在直线方程为y=±(
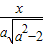 ),所以坐标原点O到直线AF1的距离为
),所以坐标原点O到直线AF1的距离为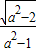 ,
,又|OF1|=
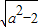 ,所以
,所以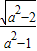 =|=
=|=
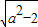 ,解得:a=2.
,解得:a=2.∴所求椭圆的方程为
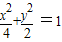 .
.(2)由题意可知直线l的斜率存在,设直线斜率为k,则直线l的方程为y=k(x+1),故M(0,k).
设Q(x1,y1),由于Q,F,三点共线,且|MQ|=|2QF|.
根据题意得(x1,y1-k)=±2(x1+1,y1),解得
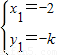 或
或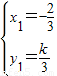
又Q在椭圆C上,故
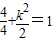 或
或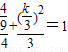 ,
,解得k=0,k=±4,综上,直线的斜率为0或±4
点评:本题主要考查了椭圆的标准方程和直线与椭圆的关系.常需要直线方程和椭圆方程联立,根据韦达定理求得问题.

练习册系列答案
相关题目

 设椭圆
设椭圆 的左右焦点分别为
的左右焦点分别为 、
、 ,
, 是椭圆
是椭圆 上的一点,且
上的一点,且 ,坐标原点
,坐标原点 到直线
到直线 的距离为
的距离为 .
. 是椭圆
是椭圆 交
交 轴于点
轴于点 ,交
,交 轴于点
轴于点 ,若
,若 ,求直线
,求直线 的左右焦点分别为
的左右焦点分别为 ,离心率
,离心率 ,点
,点 在直线
在直线 :
: 的左侧,且F2到l的距离为
的左侧,且F2到l的距离为 。
。 的值;
的值; 是
是 ,证明:当
,证明:当 取最小值时,
取最小值时, 。
。