题目内容
(2011•太原模拟)已知AC、BD为圆O:x2+y2=4的两条相互垂直的弦,垂足为M(1,
),则四边形ABCD的面积的最大值为
| 2 |
5
5
.分析:设圆心到AC、BD的距离分别为d1、d2,则 d12+d22 =3,代入面积公式s=
AC×BD,使用基本不等式求出四边形ABCD的面积的最大值.
| 1 |
| 2 |
解答: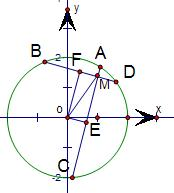 解:如图
解:如图
连接OA、OD作OE⊥AC OF⊥BD垂足分别为E、F
∵AC⊥BD
∴四边形OEMF为矩形
已知OA=OC=2 OM=
,
设圆心O到AC、BD的距离分别为d1、d2,
则d12+d22=OM2=3.
四边形ABCD的面积为:s=
•|AC|(|BM|+|MD|),
从而:
s=
|AC|•|BD|=2
≤8-(
+
)=5,
当且仅当d12 =d22时取等号,
故答案为:5.
 解:如图
解:如图连接OA、OD作OE⊥AC OF⊥BD垂足分别为E、F
∵AC⊥BD
∴四边形OEMF为矩形
已知OA=OC=2 OM=
| 3 |
设圆心O到AC、BD的距离分别为d1、d2,
则d12+d22=OM2=3.
四边形ABCD的面积为:s=
| 1 |
| 2 |
从而:
s=
| 1 |
| 2 |
(4-
|
| d | 2 1 |
| d | 2 2 |
当且仅当d12 =d22时取等号,
故答案为:5.
点评:此题考查学生掌握垂径定理及勾股定理的应用,灵活运用两点间的距离公式化简求值,是一道中档题.解答关键是四边形面积可用互相垂直的2条对角线长度之积的一半来计算.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目