题目内容
一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分.(Ⅰ)若从袋子里一次随机取出3个球,求得4分的概率;
(Ⅱ)若从袋子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分ξ的概率分布列及数学期望.
分析:(Ⅰ)由题意知本题是一个等可能事件的概率,试验发生包含的事件数C53,从袋子里一次随机取出3个球得4分表示取出的球中有1个红球和2个黑球的情况,满足条件的事件数C21C32,根据公式得到结果.
(Ⅱ)由题意,ξ的可能取值为3.4.5.6.因为是有放回地取球,所以每次取到红球的概率为
,结合变量对应的事件写出分布列和期望.
(Ⅱ)由题意,ξ的可能取值为3.4.5.6.因为是有放回地取球,所以每次取到红球的概率为
| 2 |
| 5 |
解答:解:(Ⅰ)由题意知本题是一个等可能事件的概率,
试验发生包含的事件数C53,
设“一次取出3个球得4分”的事件记为A,
它表示取出的球中有1个红球和2个黑球的情况,
满足条件的事件数C21C32
则P(A)=
=
(Ⅱ)由题意,ξ的可能取值为3.4.5.6.因为是有放回地取球,
所以每次取到红球的概率为
,取到黑球的概率为
.
P(ξ=3)=
(
)3=
P(ξ=4)=
(
)2•
=
P(ξ=5)=
(
)•(
)2=
P(ξ=6)=
(
)3=
∴ξ的分布列为
数学期望:Eξ=3×
+4×
+5×
+6×
=
试验发生包含的事件数C53,
设“一次取出3个球得4分”的事件记为A,
它表示取出的球中有1个红球和2个黑球的情况,
满足条件的事件数C21C32
则P(A)=
| ||||
|
| 3 |
| 5 |
(Ⅱ)由题意,ξ的可能取值为3.4.5.6.因为是有放回地取球,
所以每次取到红球的概率为
| 2 |
| 5 |
| 3 |
| 5 |
P(ξ=3)=
| C | 3 3 |
| 3 |
| 5 |
| 27 |
| 125 |
P(ξ=4)=
| C | 2 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 54 |
| 125 |
P(ξ=5)=
| C | 1 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 36 |
| 125 |
P(ξ=6)=
| C | 0 3 |
| 2 |
| 5 |
| 8 |
| 125 |
∴ξ的分布列为

数学期望:Eξ=3×
| 27 |
| 125 |
| 54 |
| 125 |
| 36 |
| 125 |
| 8 |
| 125 |
| 21 |
| 5 |
点评:本题考查离散型随机变量的分布列和期望,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
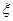 的概率分布列及数学期望。
的概率分布列及数学期望。 的概率分布列及数学期望。
的概率分布列及数学期望。