题目内容
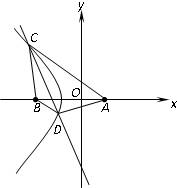
 (2009•黄冈模拟)已知A(1,0),B(-2,0),动点M满足∠MBA=2∠MAB(∠MAB≠0).
(2009•黄冈模拟)已知A(1,0),B(-2,0),动点M满足∠MBA=2∠MAB(∠MAB≠0).(1)求动点M的轨迹E的方程;
(2)若直线l:y=
| 1 | 3 |
①求实数b的取值范围;
②是否可能有A、B、C、D四点共圆?若可能,求实数b的值;若不可能,请说明理由.
分析:(1)如何体现动点M满足的条件∠MBA=2∠MAB是解决本题的关键.用动点M的坐标体现∠MBA=2∠MAB的最佳载体是直线MA、MB的斜率.
(2)先设C(x1,y1),D(x2,y2),CD的中点(x0,y0)(x1,x2,x0<-1).由点差法有y0=-x0.又y0=
x0+b;所以x0=-
b,y0=
b.又直线CD的方程为y=-3x-
b.将直线的方程代入(1)的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用到角公式即可求得b值,从而解决问题.
(2)先设C(x1,y1),D(x2,y2),CD的中点(x0,y0)(x1,x2,x0<-1).由点差法有y0=-x0.又y0=
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
解答:解:(1)设动点M的坐标为(x,y),则tan∠MBA=
,tan∠MAB=
.
 由∠MBA=2∠MAB(∠MAB≠0),得
由∠MBA=2∠MAB(∠MAB≠0),得
=
,
化简得3x2-y2=3,
当∠MBA=
时也满足.
显然,动点M在线段AB的中垂线的左侧,且∠MAB≠0,
故轨迹E的方程为 3x2-y2=3(x<-1).
(2)设C(x1,y1),D(x2,y2),CD的中点(x0,y0)(x1,x2,x0<-1).
由点差法有
•
=3,即y0=-x0.
又y0=
x0+b;所以x0=-
b,y0=
b.
①由3(-
b)2-(
b)2>3及x0=-
b<-1得,b>
.
②直线CD的方程为y-
b=-3(x-
b),即y=-3x-
b.(b≠2)
上式代入3x2-y2=3得,8x2+12bx+3b2+4=0,
所以△=16(3b2-8),x1+x2=-
b,x1x2=
,x2-x1=
.
若A、B、C、D四点共圆,则∠CAD=60°,由到角公式可得
=
即
=
,即
=
(4-b);解得b=
.
故可能有A、B、C、D四点共圆,此时b=
.
| |y| |
| x+2 |
| |y| |
| 1-x |
 由∠MBA=2∠MAB(∠MAB≠0),得
由∠MBA=2∠MAB(∠MAB≠0),得| |y| |
| x+2 |
2
| ||
1-(
|
化简得3x2-y2=3,
当∠MBA=
| π |
| 2 |
显然,动点M在线段AB的中垂线的左侧,且∠MAB≠0,
故轨迹E的方程为 3x2-y2=3(x<-1).
(2)设C(x1,y1),D(x2,y2),CD的中点(x0,y0)(x1,x2,x0<-1).
由点差法有
| y1-y2 |
| x1-x2 |
| y1+y2 |
| x1+x2 |
又y0=
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
①由3(-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 6 |
②直线CD的方程为y-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
上式代入3x2-y2=3得,8x2+12bx+3b2+4=0,
所以△=16(3b2-8),x1+x2=-
| 3 |
| 2 |
| 3b2+4 |
| 8 |
| ||
| 2 |
若A、B、C、D四点共圆,则∠CAD=60°,由到角公式可得
| y2(x1-1)-y1(x2-1) |
| (x1-1)(x2-1)+y1y2 |
| 3 |
即
(
| ||||
10x1x2+(
|
| 3 |
| 3b2-8 |
| 3 |
| 7 |
| 3 |
故可能有A、B、C、D四点共圆,此时b=
| 7 |
| 3 |
点评:求曲线的轨迹方程常采用的方法有直接法、定义法、代入法、参数法,本题主要用直接法,直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程.

练习册系列答案
相关题目
 (2009•黄冈模拟)如图是一几何体的平面展开图,其中ABCD为正方形,E、F分别为PA、PD的中点.在此几何体中,给出下面四个结论:
(2009•黄冈模拟)如图是一几何体的平面展开图,其中ABCD为正方形,E、F分别为PA、PD的中点.在此几何体中,给出下面四个结论: