题目内容
四边形ABCD是梯形,
•
=0,
与
共线,A,B是两个定点,其坐标分别为(-1,0),(1,0),C、D是两个动点,且满足|CD|=|BC|.
(Ⅰ)求动点C的轨迹E的方程;
(Ⅱ)设直线BC与动点C的轨迹E的另一交点为P,过点B且垂直于BC的直线交动点C的轨迹E于M,N两点,求四边形CMPN面积的最小值.
| AB |
| AD |
| AB |
| CD |
(Ⅰ)求动点C的轨迹E的方程;
(Ⅱ)设直线BC与动点C的轨迹E的另一交点为P,过点B且垂直于BC的直线交动点C的轨迹E于M,N两点,求四边形CMPN面积的最小值.
(Ⅰ)由
•
=0,
与
共线可知,
四边形ABCD是直角梯形,且CD⊥DA,又|CD|=|BC|,
所以动点C的轨迹为以B为焦点,DA为准线,
对称轴为x轴的抛物线.
设动点C的轨迹E的方程y2=2px(p>0),
则p=|AB|=2
所以动点C的轨迹E的方程是y2=4x(x≠0,x≠1)…(3分)
(Ⅱ)设直线BC斜率为k,
由题意知,k存在且k≠0,
直线BC的方程y=k(x-1)
依题意
,
∴k2x2-(2k2+4)x+k2=0,
设P(x1,y1),C(x2,y2)
则x1+x2=
,x1x2=1,
|PC|=
=
直线MN垂直于直线BC,
以-
替代上式中的k,得|MN|=4(k2+1)…(7分)
∴S四边形CMPN=
|PC|•|BN|+
|PC|•|BM|
=
|PC|(|BN|+|BM|)
=
|PC|•|MN|
=
•
•4(1+k2)
=8•
=8(k2+
+2)
∵k2+
≥2∴8(k2+
+2)≥32
四边形CMPN面积的最小值等于32. …(12分)
| AB |
| AD |
| AB |
| CD |
四边形ABCD是直角梯形,且CD⊥DA,又|CD|=|BC|,
所以动点C的轨迹为以B为焦点,DA为准线,
对称轴为x轴的抛物线.
设动点C的轨迹E的方程y2=2px(p>0),
则p=|AB|=2
所以动点C的轨迹E的方程是y2=4x(x≠0,x≠1)…(3分)
(Ⅱ)设直线BC斜率为k,
由题意知,k存在且k≠0,
直线BC的方程y=k(x-1)
依题意
|
∴k2x2-(2k2+4)x+k2=0,
设P(x1,y1),C(x2,y2)
则x1+x2=
| 2k2+4 |
| k2 |
|PC|=
| (1+k2)[(x1+x2)2-4x1x2] |
| 4(1+k2) |
| k2 |
直线MN垂直于直线BC,
以-
| 1 |
| k |
∴S四边形CMPN=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 4(1+k2) |
| k2 |
=8•
| k4+2k2+1 |
| k2 |
| 1 |
| k2 |
∵k2+
| 1 |
| k2 |
| 1 |
| k2 |
四边形CMPN面积的最小值等于32. …(12分)

练习册系列答案
相关题目
 如图所示,四边形ABCD是梯形,AD∥BC,则
如图所示,四边形ABCD是梯形,AD∥BC,则| OA |
| BC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
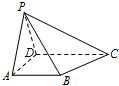 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面四边形ABCD是梯形,AB∥DC,BC=DC=2AB=2,
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面四边形ABCD是梯形,AB∥DC,BC=DC=2AB=2,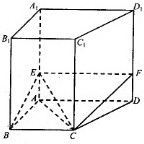 (2010•南京三模)如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是梯形,AD∥BC,AC⊥CD,E是AA1上的一点.
(2010•南京三模)如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是梯形,AD∥BC,AC⊥CD,E是AA1上的一点.