Question

△ABC所在平面α外有一点P，过P作PO⊥α，垂足为O，连结PA、PB、PC.

(1)若PA=PB=PC，则O为△ABC的　　　　　心；

(2)若PA⊥PB，PB⊥PC，PC⊥PA，则O为△ABC的?　　　　　?心；

(3)P到三边AB、BC、CA的距离相等，则O为△ABC的?　　　　　?心；

(4)若PA=PB=PC，∠C=90°，则O是AB边的　　　　点；

(5)若PA=PB=PC，AB=AC，则O点在　　　　　线上.

Answer 1

解析：(1)如图，∵PO⊥α,PA=PB=PC，由射影定理不难得到OA=OB=OC，即O是外心.?

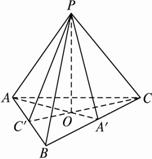
(2)如图，由条件PA、PB、PC两两垂直可得AP⊥面PBCPA⊥BCBC⊥AA′，同理可得AB⊥CC′，由此可知O为垂心.?

(3)如图，若PA′⊥BC,PC′⊥AB?CO⊥AB,AO⊥BC.?

又PA′=PC′OC′=OA′，可知O为内心.?

(4)由(1)知O为△ABC的外心，而△ABC为直角三角形,故O为AB的中点.?

(5)由(1)知O为△ABC的外心，而AB=AC，故O在△ABC的边BC的中线上(或高或∠BAC的平分线).

答案：(1)外　(2)垂　(3)内　(4)中　(5)中