题目内容
若2α与2β互余,则(1+tanα)(1+tanβ)的值为( )A.1
B.2
C.3
D.4
【答案】分析:由2α与2β互余,得到2α与2β之和为90°,可得出α与β之和为45°,利用特殊角的三角函数值求出tan(α+β)的值,再利用两角和与差的正切函数公式化简tan(α+β),得到一个关系式,将所求的式子去括号整理后,把得到的关系式代入计算,即可求出值.
解答:解:∵2α与2β互余,即2α+2β=90°,
∴α+β=45°,
∴tan(α+β)=1,又tan(α+β)=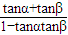 ,
,
∴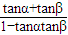 =1,即tanα+tanα=1-tanαtanβ,
=1,即tanα+tanα=1-tanαtanβ,
则(1+tanα)(1+tanβ)=1+tanβ+tanα+tanαtanβ=2.
故选B
点评:此题考查了两角和与差的正切函数公式,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.
解答:解:∵2α与2β互余,即2α+2β=90°,
∴α+β=45°,
∴tan(α+β)=1,又tan(α+β)=
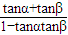 ,
,∴
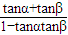 =1,即tanα+tanα=1-tanαtanβ,
=1,即tanα+tanα=1-tanαtanβ,则(1+tanα)(1+tanβ)=1+tanβ+tanα+tanαtanβ=2.
故选B
点评:此题考查了两角和与差的正切函数公式,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目