题目内容
过点P（3，4）的动直线与两坐标轴的交点分别为A，B，过A，B分别作两坐标轴的垂线交于点M，则点M的轨迹方程为 ．
【答案】分析：设出M坐标，求出A，B坐标，利用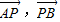
共线，求出x，y的关系式，就是所求M的轨迹方程．
解答：解：设M（x，y）由题意可知A（x，0），B（0，y），
因为A，B，P三点共线，所以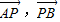
共线，
，
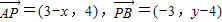所以（3-x）（y-4）=-12，即4x+3y=xy，
所以点M的轨迹方程为：4x+3y=xy．
故答案为：4x+3y=xy．
点评：本题考查曲线轨迹方程的求法，考查转化思想计算能力．
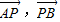共线，求出x，y的关系式，就是所求M的轨迹方程．解答：解：设M（x，y）由题意可知A（x，0），B（0，y），
因为A，B，P三点共线，所以
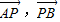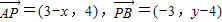共线，，所以（3-x）（y-4）=-12，即4x+3y=xy，
所以点M的轨迹方程为：4x+3y=xy．
故答案为：4x+3y=xy．
点评：本题考查曲线轨迹方程的求法，考查转化思想计算能力．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
已知过点A（-1，0）的动直线l与圆C：x2+（y-3）2=4相交于P，Q两点，M是PQ的中点，l与直线m：x+3y+6=0相交于点N，则下面运算结果为定值的有（ ）