题目内容
四棱锥P-ABCD中,PA⊥平面ABCD,底面是平行四边形,PA=AD=2a,AB=a,AC=
a.
(1)求证:平面PDC⊥平面APC;
(2)求异面直线PC与BD所成角的余弦值;
(3)求二面角A-PC-B的正切值.
| 3 |
(1)求证:平面PDC⊥平面APC;
(2)求异面直线PC与BD所成角的余弦值;
(3)求二面角A-PC-B的正切值.
分析:(1)先证⇒∠ADC为直角,利用PA⊥平面ABCD证明 DC⊥PA,这样,DC⊥平面PAD,进而证明面PDC⊥平面APC.
(2)设AC与BD的交点为O,取AP的中点E,∠EOB就是异面直线PC与BD所成的角或补角,解三角形求此角的大小.
(3)根据AB⊥面PAC,过A作AF⊥PC,由三垂线定理可知BF⊥PC,∠AFB就是二面角A-PC-B的平面角,解三角形.
求出此角的大小.
(2)设AC与BD的交点为O,取AP的中点E,∠EOB就是异面直线PC与BD所成的角或补角,解三角形求此角的大小.
(3)根据AB⊥面PAC,过A作AF⊥PC,由三垂线定理可知BF⊥PC,∠AFB就是二面角A-PC-B的平面角,解三角形.
求出此角的大小.
解答:(1)证:∵AD=2a,AB=a,AC=
a⇒∠ADC为直角,
⇒
⇒
⇒面PCD⊥PCA
(2)解:设AC与BD的交点为O,取AP的中点E,
连OE,BE,OB=OE=
a,BE=
a,
∵EO∥PC,∴∠EOB就是异面直线PC与BD所成的角或补角.
cos∠EOB=
=
=
.
(3)解:∵AB⊥面PAC,过A作AF⊥PC,连BF,
由三垂线定理可知BF⊥PC,
∴∠AFB就是二面角A-PC-B的平面角.
∵AF•PC=PA•AC,∴AF=
=
a,
∴tan∠AFB=
=
.
| 3 |
|
|
|
(2)解:设AC与BD的交点为O,取AP的中点E,
连OE,BE,OB=OE=
| ||
| 2 |
| 2 |
∵EO∥PC,∴∠EOB就是异面直线PC与BD所成的角或补角.
cos∠EOB=
| ||||||||
2•
|
| ||
|
| 3 |
| 7 |
(3)解:∵AB⊥面PAC,过A作AF⊥PC,连BF,
由三垂线定理可知BF⊥PC,
∴∠AFB就是二面角A-PC-B的平面角.
∵AF•PC=PA•AC,∴AF=
2a•
| ||
|
2
| ||
|
∴tan∠AFB=
| a | ||||||
|
| ||
| 6 |
点评:本题考查利用面面垂直的判定定理证明面面垂直,通过转化,把空间角转化为两条相交直线成的角,解三角形求出此角的大小.

练习册系列答案
相关题目
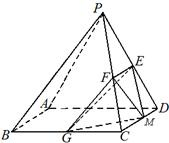 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.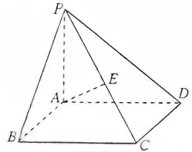 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2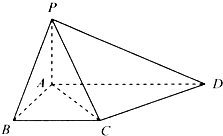 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.