题目内容
已知数列{an}的前n项和为Sn,且a1= ,an+1=Sn+
,an+1=Sn+ (n∈N*,t为常数).
(n∈N*,t为常数).(Ⅰ)若数列{an}为等比数列,求t的值;
(Ⅱ)若t>-4,bn=lgan+1,数列{bn}前n项和为Tn,当且仅当n=6时Tn取最小值,求实数t的取值范围.
【答案】分析:(Ⅰ)利用数列递推式,再写一式,两式相减,结合数列{an}为等比数列,即可求t的值;
(Ⅱ)确定数列{bn}是等差数列,利用当且仅当n=6时,Tn取最小值,可得b6<0且b7>0,解不等式,即可求t的取值范围.
解答:解:(I)∵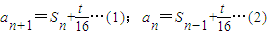
(1)-(2)得:an+1=2an(n≥2)…(2分)
∵数列{an}为等比数列,∴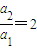 …..(4分)
…..(4分)
∵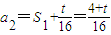 ,a1=
,a1= ,
,
∴ ,∴t=4…(6分)
,∴t=4…(6分)
(II)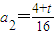 ,an+1=2an(n>1),∴
,an+1=2an(n>1),∴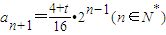 ….(8分)
….(8分)
∵a2,a3,a4…an+1成等比数列,bn=lgan+1,
∴数列{bn}是等差数列
∵数列{bn}前n项和为Tn,当且仅当n=6时,Tn取最小值,∴b6<0且b7>0…(10分)
可得0<a7<1且a8>1,…(12分)
∴0<16+4t<1且32+2t>1,
∴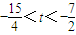 …(14分)
…(14分)
点评:本题考查数列递推式,考查等差数列与等比数列的综合,考查学生分析解决问题的能力,属于中档题.
(Ⅱ)确定数列{bn}是等差数列,利用当且仅当n=6时,Tn取最小值,可得b6<0且b7>0,解不等式,即可求t的取值范围.
解答:解:(I)∵
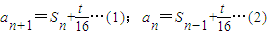
(1)-(2)得:an+1=2an(n≥2)…(2分)
∵数列{an}为等比数列,∴
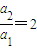 …..(4分)
…..(4分)∵
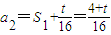 ,a1=
,a1= ,
,∴
 ,∴t=4…(6分)
,∴t=4…(6分)(II)
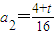 ,an+1=2an(n>1),∴
,an+1=2an(n>1),∴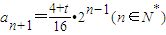 ….(8分)
….(8分)∵a2,a3,a4…an+1成等比数列,bn=lgan+1,
∴数列{bn}是等差数列
∵数列{bn}前n项和为Tn,当且仅当n=6时,Tn取最小值,∴b6<0且b7>0…(10分)
可得0<a7<1且a8>1,…(12分)
∴0<16+4t<1且32+2t>1,
∴
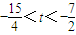 …(14分)
…(14分)点评:本题考查数列递推式,考查等差数列与等比数列的综合,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |